The Kingdom of Childhood

APPENDIX TO LECTURE 5

I. Proof for the Theorem of Pythagoras.

(As it has been impossible to reproduce the diagrams in colour, the forms which Dr. Steiner referred to by their colours have been indicated by letters or numbers.) It is quite easy to do this proof if the triangle is isosceles. If you have here a right-angled isosceles triangle (see diagram a.), then this is one side, this is the other and this the hypotenuse. This square (1, 2, 3, 4) is the square on the hypotenuse. The squares (2, 5) and (4, 6) are the squares on the other two sides.

Now if I plant potatoes evenly in these two fields (2, 5) and (4, 6), I shall get just as many as if I plant potatoes in

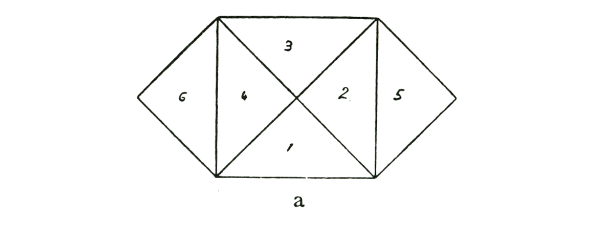
this field (1, 2, 3, 4). (1, 2, 3, 4) is the square on the hypotenuse, and the two fields (2, 5) and (4, 6) are the squares on the other two sides.

You can make the proof quite obvious by saying: the parts (2) and (4) of the two smaller squares fall into this space here (1, 2, 3, 4, the square on the hypotenuse); they are already within it. The part (5) exactly fits in to the space (3), and if you cut out the whole thing you can take the triangle (6) and apply it to (1), and you will see at once that it is the same. So that the proof is quite clear if you have a so-called right-angled isosceles triangle.

If however you have a triangle that is not isosceles, but has unequal sides (see diagram b.), you can do it as follows:

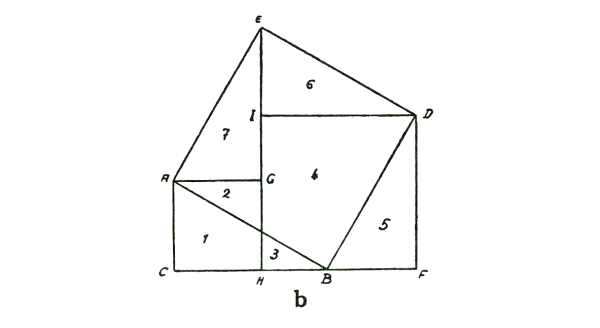
draw the triangle again ABC; then draw the square on the hypotenuse ABDE. Proceed as follows: draw the triangle ABC again over here, DBF. Then this triangle ABC or DBF (which is the same), can be put up there, AGE. Since you now have this triangle repeated over there, you can draw the square over one of the other sides, CAGH.

As you see, I can now also draw this triangle DEI congruent to BCA. Then the square DIHF is the square on the other side. Here I have both the square on the one side and the square on the other side. In the one case I use the side AG and in the other case the side DI. The two triangles AEG and DEI are congruent. Where is then the square on the hypotenuse? It is the square ABDE. Now I have to show from the figure itself that (1, 2) and (3, 4, 5) together make up (2, 4, 6, 7). Now I first take the square (1, 2); this has the triangle (2) in common with the square on the hypotenuse ABDE and section (4) of the square on the other side HIDF is also contained in ABDE. Thus I get this figure (2, 4) which you see drawn here and which is actually a piece of the square ABDE. This only leaves parts (1, 3 and 5) of the squares AGHC and DIHF to be fitted into the square on the hypotenuse ABDE. Now you can take part (5) and lay it over part (6), but you will still have this corner (1, 3) left over. If you cut this out you will discover that these two areas (1, 3) fit into this area (7). Of course it can be drawn more clearly but I think you will understand the process.