FIRST LECTURE
Stuttgart, 23rd December 1919.
My dear Friends,
After the words which
have just been read out, some of which were written over 30 years
ago, I would like to say that in the short time at our disposal I
shall at most be able to contribute a few side-lights which may help
you in forming your outlook upon Nature. I hope that in no very
distant future we shall be able to continue. On this occasion, as you
must also realize, I was only told that this lecture-course was
hoped-for after my arrival here. What I can therefore give during
these days will be no more than an episode.
What I am hoping to
contribute may well be of use to those of you who are teachers and
educators, — not to apply directly in your lessons, but as a
fundamental trend and tendency in Science, which should permeate your
teaching. In view of all the aberrations to which the Science of
Nature in our time has been subject, for the teacher and educator it
is of great importance to have the right direction of ideas, at any
rate in the background.
To the words which our
friend Dr. Stein has kindly been recalling, I may add one more. It
was in the early nineties. The “Frankfurter Freier
Hochstift” had invited me to speak on Goethe's work in Science.
I then said in introduction that I should mainly confine myself to
his work in the organic Sciences. For to carry Goethe's
world-conception into our physical and chemical ideas, was as yet
quite impossible. Through all that lives and works in the Physics and
Chemistry of today, our scientists are fated in regard, whatever
takes its start from Goethe in this realm, as being almost
unintelligible from their point of view. Thus, I opined, we shall
have to wait till physicists and chemists will have witnessed —
by their own researches — a kind of “reductio ad
absurdum” of the existing theoretic structure of their Science.
Then and then only will Goethe's outlook come into its own, also in
this domain.
I shall attempt in
these lectures to establish a certain harmony between what we may
call the experimental side of Science and what concerns the outlook,
the idea, the fundamental views which we can gain on the results of
experiment. Today, by way of introduction, — and, as the saying
goes, “theoretically” — I will put forward certain
aspects that shall help our understanding. In today's lecture it will
be my specific aim to help you understand that contrast between the
current, customary science and the kind of scientific outlook which
can be derived from Goethe's general world-outlook. We must begin by
reflecting, perhaps a little theoretically, upon the premisses of
present-day scientific thinking altogether. The scientists who think
of Nature in the customary manner of our time, generally have no very
clear idea of what constitutes the field of their researches.
“Nature” has grown to be a rather vague and undefined
conception. Therefore we will not take our start from the prevailing
idea of what Nature is, but from the way in which the scientist of
modern time will generally work. Admittedly, this way of working is
already undergoing transformation, and there are signs which we may
read as the first dawning of a new world-outlook. Yet on the whole,
what I shall characterize (though in a very brief introductory
outline) may still be said to be prevailing.
The scientist today
seeks to approach Nature from three vantage-points. In the first
place he is at pains to observe Nature in such a way that from her
several creatures and phenomena he may form concepts of species, kind
and genus. He sub-divides and classifies the beings and phenomena of
Nature. You need only recall how in external, sensory experience so
many single wolves, single hyenas, single phenomena of warmth, single
phenomena of electricity are given to the human being, who thereupon
attempts to gather up the single phenomena into kinds and species. So
then he speaks of the species “wolf” or
“hyena”, likewise he classifies the phenomena into
species, thus grouping and comprising what is given, to begin with,
in many single experiences. Now we may say, this first important
activity is already taken more or less unconsciously for granted.
Scientists in our time do not reflect that they should really examine
how these “universals”, these general ideas, are related
to the single data.
The second thing, done
by the man of today in scientific research, is that he tries by
experiment, or by conceptual elaboration of the results of
experiment, to arrive at what he calls the “causes” of
phenomena. Speaking of causes, our scientists will have in mind
forces or substances or even more universal entities. They speak for
instance of the force of electricity, the force of magnetism, the
force of heat or warmth, and so on. They speak of an unknown
“ether” or the like, as underlying the phenomena of light
and electricity. From the results of experiment they try to arrive at
the properties of this ether. Now you are well aware how very
controversial is all that can be said about the “ether”
of Physics. There is one thing however to which we may draw attention
even at this stage. In trying, as they put it, to go back to the
causes of phenomena, the scientists are always wanting to find their
way from what is known into some unknown realm. They scarcely ever
ask if it is really justified thus to proceed from the known to the
unknown. They scarcely trouble, for example, to consider if it is
justified to say that when we perceive a phenomenon of light or
colour, what we subjectively describe as the quality of colour is the
effect on us, upon our soul, our nervous apparatus, of an objective
process that is taking place in the universal ether — say a
wave-movement in the ether. They do not pause to think, whether it is
justified thus to distinguish (what is what they really do) between
the “subjective” event and the “objective”,
the latter being the supposed wave-movement in the ether, or else the
interaction thereof with processes in ponderable matter.
Shaken though it now
is to some extent, this kind of scientific outlook was predominant in
the 19th century, and we still find it on all hands in the whole way
the phenomena are spoken of; it still undoubtedly prevails in
scientific literature to this day.
Now there is also a
third way in which the scientist tries to get at the configuration of
Nature. He takes the phenomena to begin with — say, such a
simple phenomenon as that a stone, let go, will fall to earth, or if
suspended by a string, will pull vertically down towards the earth.
Phenomena like this the scientist sums up and so arrives at what he
calls a “Law of Nature”. This statement for example would
be regarded as a simple “Law of Nature”: “Every
celestial body attracts to itself the bodies that are upon it”.
We call the force of attraction Gravity or Gravitation and then
express how it works in certain “Laws”. Another classical
example are the three statements known as “Kepler's
Laws”.
It is in these three
ways that “scientific research” tries to get near to
Nature. Now I will emphasize at the very outset that the Goethean
outlook upon Nature strives for the very opposite in all three
respects. In the first place, when he began to study natural
phenomena, the classification into species and genera, whether of the
creatures or of the facts and events of Nature, at once became
problematical for Goethe. He did not like to see the many concrete
entities and facts of Nature reduced to all these rigid concepts of
species, family and genus; what he desired was to observe the gradual
transition of one phenomenon into another, or of one form of
manifestation of an entity into another. He felt concerned, not with
the subdivision and classification into genera, but with the
metamorphosis both of phenomena and of the several creatures. Also
the quest of so-called “causes” in Nature, which Science
has gone on pursuing ever since his time, was not according to
Goethe's way of thinking. In this respect it is especially important
for us to realize the fundamental difference between natural science
and research as pursued today and on the other hand the Goethean
approach to Nature.
The Science of our
time makes experiments; having thus studied the phenomena, it then
tries to form ideas about the so-called causes that are supposed to
be there behind them; — behind the subjective phenomenon of
light or colour for example, the objective wave-movement in the
ether. Not in this style did Goethe apply scientific thinking. In his
researches into Nature he does not try to proceed from the so-called
“known” to the so-called “unknown”. He always
wants to stay within the sphere of what is known, nor in the first
place is he concerned to enquire whether the latter is merely
subjective, or objective. Goethe does not entertain such concepts as
of the “subjective” phenomena of colour and the
“objective” wave-movements in outer space. What he
beholds spread out in space and going on in time is for him one, a
single undivided whole. He does not face it with the question,
subjective or objective? His use of scientific thinking and
scientific method is not to draw conclusions from the known to the
unknown; he will apply all thinking and all available methods to put
the phenomena themselves together till in the last resort he gets the
kind of phenomena which he calls archetypal, — the
Ur-phenomena. These archetypal phenomena — once more,
regardless of “subjective or objective” — bring to
expression what Goethe feels is fundamental to a true outlook upon
Nature and the World. Goethe therefore remains amid the sequence of
actual phenomena; he only sifts and simplifies them and then calls
“Ur-phenomenon” the simplified and clarified phenomenon,
ideally transparent and comprehensive.
Thus Goethe looks upon
the whole of scientific method — so to call it — purely
and simply as a means of grouping the phenomena. Staying amid the
actual phenomena, he wants to group them in such a way that they
themselves express their secrets. He nowhere seeks to recur from the
so-called “known” to an “unknown” of any
kind. Hence too for Goethe in the last resort there are not what may
properly be called “Laws of Nature”. He is not looking
for such Laws. What he puts down as the quintessence of his
researches are simple facts — the fact, for instance, of how
light will interact with matter that is in its path. Goethe puts into
words how light and matter interact. That is no “law”; it
is a pure and simple fact. And upon facts like this he seeks to base
his contemplation, his whole outlook upon Nature. What he desires,
fundamentally, is a rational description of Nature. Only for him
there is a difference between the mere crude description of a
phenomenon as it may first present itself, where it is complicated
still and untransparent, and the description which emerges when one
has sifted it, so that the simple essentials and they alone stand
out. This then — the Urphenomenon — is what Goethe takes
to be fundamental, in place of the unknown entities or the
conceptually defined “Laws” of customary Science.
One fact may throw
considerable light on what is seeking to come into our Science by way
of Goetheanism, and on what now obtains in Science. It is remarkable:
few men have ever had so clear an understanding of the relation of
the phenomena of Nature to mathematical thinking as Goethe had.
Goethe himself not having been much of a mathematician, this is
disputed no doubt. Some people think he had no clear idea of the
relation of natural phenomena to those mathematical formulations
which have grown ever more beloved in Science, so much so that in our
time they are felt to be the one and only firm foundation.
Increasingly in modern time, the mathematical way of studying the
phenomena of Nature — I do not say directly, the mathematical
study of Nature; it would not be right to put it in these words, but
the study of natural phenomena in terms of mathematical formulae
— has grown to be the determining factor in the way we think
even of Nature herself.
Concerning these
things we really must reach clarity. You see, dear Friends, along the
accustomed way of approach to Nature we have three things to begin
with — things that are really exercised by man before he
actually reaches Nature. The first is common or garden Arithmetic. In
studying Nature nowadays we do a lot of arithmetic — counting
and calculating. Arithmetic — we must be clear on this —
is something man understands on its own ground, in and by itself.
When we are counting it makes no difference what we count. Learning
arithmetic, we receive something which, to begin with, has no
reference to the outer world. We may count peas as well as electrons.
The way we recognize that our methods of counting and calculating are
correct is altogether different from the way we contemplate and form
conclusions about the outer processes to which our arithmetic is then
applied.
The second of the
three to which I have referred is again a thing we do before we come
to outer Nature. I mean Geometry, — all that is known by means
of pure Geometry. What a cube or an octahedron is, and the relations
of their angles, — all these are things which we determine
without looking into outer Nature. We spin and weave them out of
ourselves. We may make outer drawings on them, but this is only to
serve mental convenience, not to say inertia. Whatever we may
illustrate by outer drawings, we might equally well imagine purely in
the mind. Indeed it is very good for us to imagine more of these
things purely in the mind, using the crutches of outer illustration
rather less. Thus, what we have to say concerning geometrical form is
derived from a realm which, to begin with, is quite away from outer
Nature. We know what we have to say about a cube without first having
had to read it in a cube of rock-salt. Yet in the latter we must find
it. So we ourselves do something quite apart from Nature and then
apply it to the latter.
And then there is the
third thing which we do, still before reaching outer Nature. I am
referring to what we do in “Phoronomy” so-called, or
Kinematics, i.e. the science of Movement. Now it is very important
for you to be clear on this point, — to realize that Kinematics
too is, fundamentally speaking, still remote from what we call the
“real” phenomena of Nature. Say I imagine an object to be
moving from the point a to the point b (Figure
Ia). I am not looking at any moving object; I just imagine it.
Then I can always imagine this movement from a to
b, indicated by an arrow in the figure, to be compounded of
two distinct movements. Think of it thus: the point a is ultimately
to get to b, but we suppose it does not go there at once. It
sets out in this other direction and reaches c. If it then
subsequently moves from c to b, it does eventually
get to b. Thus I can also imagine the movement from
a to b so that it does not go along the line a
— b but along the line, or the two lines, a — c
— b. The movement ab is then compounded of the
movements ac and cb, i.e. of two distinct
movements. You need not observe any process in outer Nature; you can
simply think it — picture it to yourself in thought — how
that the movement from a to b is composed of the
two other movements. That is to say, in place of the one movement the
two other movements might be carried out with the same ultimate
effect. And when in thinking I picture this. The thought — the
mental picture — is spun out of myself. I need have made no
outer drawing; I could simply have instructed you in thought to form
the mental picture; you could not but have found it valid. Yet if in
outer Nature there is really something like the point a
— perhaps a little ball, a grain of shot — which in one
instance moves from a to b and in another from
a to c and then from c to b, what
I have pictured to myself in thought will really happen. So then it
is in kinematics, in the science of movement also; I think the
movements to myself, yet what I think proves applicable to the
phenomena of Nature and must indeed hold good among them.
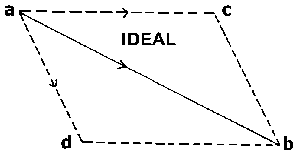
Figure Ia |
|
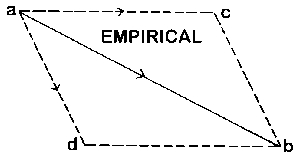
Figure Ib |
Thus we may truly say:
In Arithmetic, in Geometry and in Phoronomy or Kinematics we have the
three preliminary steps that go before the actual study of Nature.
Spun as they are purely out of ourselves, the concepts which we gain
in all these three are none the less valid for what takes place in
real Nature.
And now I beg you to
remember the so-called Parallelogram of forces, (Figure
Ib). This time, the point a will signify a material thing —
some little grain of material substance. I exert a force to draw it
on from a to b. Mark the difference between the way
I am now speaking and the way I spoke before. Before, I spoke of
movement as such; now I am saying that a force draws the little ball
from a to b. Suppose the measure of this force,
pulling from a to b, to be five grammes; you can
denote it by a corresponding length in this direction. With a force
of five grammes I am pulling the little ball from a to
b. Now I might also do it differently. Namely I might first
pull with a certain force from a to c. Pulling from
a to c (with a force denoted by this length) I need
a different force than when I pulled direct from a to
b. Then I might add a second pull, in the direction of the
line from c to b, and with a force denoted by the
length of this line. Having pulled in the first instance from a
towards b with a force of five grammes, I should have to
calculate from this figure, how big the pull a — c and
also how big the pull c — d would have to be. Then if
I pulled simultaneously with forces represented by the lines a
— c and a — d of the parallelogram, I
should be pulling the object along in such a way that it eventually
got to b; thus I can calculate how strongly I must pull
towards c and d respectively. Yet I cannot
calculate this in the same way as I did the displacements in our
previous example. What I found previously (as to the movement pure
and simple), that I could calculate, purely in thought. Not so when a
real pull, a real force is exercised. Here I must somehow measure the
force; I must approach Nature herself; I must go on from thought to
the world of facts. If once you realize this difference between the
Parallelogram of
Movements and that of
Forces, you have a clear and sharp formulation of the essential
difference between all those things that can be determined within the
realm of thought, and those that lie beyond the range of thoughts and
mental pictures. You can reach movements but not forces with your
mental activity. Forces you have to measure in the outer world. The
fact that when two pulls come into play — the one from
a to c, the other from a to d,
— the thing is actually pulled from a to b
according to the
Parallelogram of Forces, this you cannot make sure of in any
other way than by an outer experiment. There is no proof by dint of
thought, as for the
Parallelogram of Movements. It must be measured and ascertained
externally. Thus in conclusion we may say: while we derive the
parallelogram of movements by pure reasoning, the parallelogram of
forces must be derived empirically, by dint of outer experience.
Distinguishing the parallelogram of movements and that of forces, you
have the difference — clear and keen — between Phoronomy
and Mechanics, or Kinematics and Mechanics. Mechanics has to do with
forces, no mere movements; it is already a Natural Science. Mechanics
is concerned with the way forces work in space and time. Arithmetic,
Geometry and Kinematics are not yet Natural Sciences in the proper
sense. To reach the first of the Natural Sciences, which is
Mechanics, we have to go beyond the life of ideas and mental
pictures.
Even at this stage our
contemporaries fail to think clearly enough. I will explain by an
example, how great is the leap from kinematics into mechanics. The
kinematical phenomena can still take place entirely within a space of
our own thinking; mechanical phenomena on the other hand must first
be tried and tested by us in the outer world. Our scientists however
do not envisage the distinction clearly. They always tend rather to
confuse what can still be seen in purely mathematical ways, and what
involves realities of the outer world. What, in effect, must be
there, before we can speak of a parallelogram of forces? So long as
we are only speaking of the parallelogram of movements, no actual
body need be there; we need only have one in our thought. For the
parallelogram of forces on the other hand there must be a mass
— a mass, that possesses weight among other things. This you
must not forget. There must be a mass at the point a, to begin with.
Now we may well feel driven to enquire: What then is a mass? What is
it really? And we shall have to admit: Here we already get stuck! The
moment we take leave of things which we can settle purely in the
world of thought so that they then hold good in outer Nature, we get
into difficult and uncertain regions. You are of course aware how
scientists proceed. Equipped with arithmetic, geometry and
kinematics, to which they also add a little dose of mechanics, they
try to work out a mechanics of molecules and atoms; for they imagine
what is called matter to be thus sub-divided, In terms of this
molecular mechanics they then try to conceive the phenomena of
Nature, which, in the form in which they first present themselves,
they regard as our own subjective experience.
We take hold of a warm
object, for example. The scientist will tell us: What you are calling
the heat or warmth is the effect on your own nerves. Objectively,
there is the movement of molecules and atoms. These you can study,
after the laws of mechanics. So then they study the laws of
mechanics, of atoms and molecules; indeed, for a long time they
imagined that by so doing they would at last contrive to explain all
the phenomena of Nature. Today, of course, this hope is rather
shaken. But even if we do press forward to the atom with our
thinking, even then we shall have to ask — and seek the answer
by experiment — How are the forces in the atom? How does the
mass reveal itself in its effects, — how does it work? And if
you put this question, you must ask again: How will you recognize it?
You can only recognize the mass by its effects.
The customary way is
to recognize the smallest unit bearer of mechanical force by its
effect, in answering this question: If such a particle brings another
minute particle — say, a minute particle of matter weighing one
gramme — into movement, there must be some force proceeding
from the matter in the one, which brings the other into movement. If
then the given mass brings the other mass, weighing one gramme, into
movement in such a way that the latter goes a centimetre a second
faster in each successive second, the former mass will have exerted a
certain force. This force we are accustomed to regard as a kind of
universal unit. If we are then able to say of some force that it is
so many times greater than the force needed to make a gramme go a
centimetre a second quicker every second, we know the ratio between
the force in question and the chosen universal unit. If we express it
as a weight, it is 0.001019 grammes' weight. Indeed, to express what
this kind of force involves, we must have recourse to the balance
— the weighing-machine. The unit force is equivalent to the
downward thrust that comes into play when 0.001019 grammes are being
weighed. So then I have to express myself in terms of something very
outwardly real if I want to approach what is called
“mass” in this Universe. Howsoever I may think it out, I
can only express the concept “mass” by introducing what I
get to know in quite external ways, namely a weight. In the last
resort, it is by a weight that I express the mass, and even if I then
go on to atomize it, I still express it by a weight.
I have reminded you of
all this, in order clearly to describe the point at which we pass,
from what can still be determined “a priori”, into the
realm of real Nature. We need to be very clear on this point. The
truths of arithmetic, geometry and kinematics, — these we
undoubtedly determine apart from external Nature. But we must also be
clear, to what extent these truths are applicable to that which meets
us, in effect, from quite another side — and, to begin with, in
mechanics. Not till we get to mechanics, have we the content of what
we call “phenomenon of Nature”.
All this was clear to
Goethe. Only where we pass on from kinematics to mechanics can we
begin to speak at all of natural phenomena. Aware as he was of this,
he knew what is the only possible relation of Mathematics to Natural
Science, though Mathematics be ever so idolized even for this domain
of knowledge.
To bring this home, I
will adduce one more example. Even as we may think of the unit
element, for the effects of Force in Nature, as a minute atom-like
body which would be able to impart an acceleration of a centimetre
per second per second to a gramme-weight, so too with every
manifestation of Force, we shall be able to say that the force
proceeds from one direction and works towards another. Thus we may
well grow accustomed — for all the workings of Nature —
always to look for the points from which the forces proceed.
Precisely this has grown habitual, nay dominant, in Science. Indeed
in many instances we really find it so. There are whole fields of
phenomena which we can thus refer to the points from which the
forces, dominating the phenomena, proceed. We therefore call such
forces “centric forces”, inasmuch as they always issue
from point-centres. It is indeed right to think of centric forces
wherever we can find so many single points from which quite definite
forces, dominating a given field of phenomena, proceed. Nor need the
forces always come into play. It may well be that the point-centre in
question only bears in it the possibility, the potentiality as it
were, for such a play of forces to arise, whereas the forces do not
actually come into play until the requisite conditions are fulfilled
in the surrounding sphere. We shall have instances of this during the
next few days. It is as though forces were concentrated at the points
in question, — forces however that are not yet in action. Only
when we bring about the necessary conditions, will they call forth
actual phenomena in their surroundings. Yet we must recognize that in
such point or space forces are concentrated, able potentially to work
on their environment.
This in effect is what
we always look for, when speaking of the World in terms of Physics.
All physical research amounts to this: we follow up the centric
forces to their centres; we try to find the points from which effects
can issue, For this kind of effect in Nature, we are obliged to
assume that there are centres, charged as it were with possibilities
of action in certain directions. And we have sundry means of
measuring these possibilities of action; we can express in stated
measures, how strongly such a point or centre has the potentiality of
working. Speaking in general terms, we call the measure of a force
thus centred and concentrated a “potential” or
“potential force”. In studying these effects of Nature we
then have to trace the potentials of the centric forces, — so
we may formulate it. We look for centres which we then investigate as
sources of potential forces.
Such, in effect, is
the line taken by that school of Science which is at pains to express
everything in mechanical terms. It looks for centric forces and their
potentials. In this respect our need will be to take one essential
step — out into actual Nature — whereby we shall grow
fully conscious of the fact: You cannot possibly understand any
phenomenon in which Life plays a part if you restrict yourself to
this method, looking only for the potentials of centric forces. Say
you were studying the play of forces in an animal or vegetable embryo
or germ-cell; with this method you would never find your way. No
doubt it seems an ultimate ideal to the Science of today, to
understand even organic phenomena in terms of potentials, of centric
forces of some kind. It will be the dawn of a new world-conception in
this realm when it is recognized that the thing cannot be done in
this way, Phenomena in which Life is working can never be understood
in terms of centric forces. Why, in effect, — why not?
Diagrammatically, let us here imagine that we are setting out to
study transient, living phenomena of Nature in terms of Physics. We
look for centres, — to study the potential effects that may go
out from such centres. Suppose we find the effect. If I now calculate
the potentials, say for the three points a, b and
c, I find that a will work thus and thus on
A, B and C, or c on A',
B' and C'; and so on. I should thus get a notion of
how the integral effects will be, in a certain sphere, subject to the
potentials of such and such centric forces. Yet in this way I could
never explain any process involving Life. In effect, the forces that
are essential to a living thing have no potential; they are not
centric forces. If at a given point d you tried to trace the
physical effects due to the influences of a, b and
c, you would indeed be referring to the effects to centric
forces, and you could do so. But if you want to study the effects of
Life you can never do this. For these effects, there are no centres
such as a or b or c. Here you will only
take the right direction with your thinking when you speak thus: Say
that at d there is something alive. I look for the forces to
which the life is subject. I shall not find them in a, nor
in b, nor in c, nor when I go still farther out. I
only find them when as it were I go to the very ends of the world
— and, what is more, to the entire circumference at once.
Taking my start from d, I should have to go to the outermost
ends of the Universe and imagine forces to the working inward from
the spherical circumference from all sides, forces which in their
interplay unite in d. It is the very opposite of the centric
forces with their potentials. How to calculate a potential for what
works inward from all sides, from the infinitudes of space? In the
attempt, I should have to dismember the forces; one total force would
have to be divided into ever smaller portions. Then I should get
nearer and nearer the edge of the World: — the force would be
completely sundered, and so would all my calculation. Here in effect
it is not centric forces; it is cosmic, universal forces that are at
work. Here, calculation ceases.
Once more, you have
the leap — the leap, this time, from that in Nature which is
not alive to that which is. In the investigation of Nature we shall
only find our way aright if we know what the leap is from Kinematics
to Mechanics, and again what the leap is from external, inorganic
Nature into those realms that are no longer accessible to
calculation, — where every attempted calculation breaks asunder
and every potential is dissolved away. This second leap will take us
from external inorganic Nature into living Nature, and we must
realize that calculation ceases where we want to understand what is
alive.
Now in this
explanation I have been neatly dividing all that refers to potentials
and centric forces and on the other hand all that leads out into the
cosmic forces. Yet in the Nature that surrounds us they are not thus
apart. You may put the question: Where can I find an object where
only centric forces work with their potentials, and on the other hand
where is the realm where cosmic forces work, which do not let you
calculate potentials? An answer can indeed be given, and it is such
as to reveal the very great importance of what is here involved. For
we may truly say: All that Man makes by way of machines — all
that is pieced together by Man from elements supplied by Nature
— herein we find the purely centric forces working, working
according to their potentials. What is existing in Nature outside us
on the other hand — even in inorganic Nature — can never
be referred exclusively to centric forces. In Nature there is no such
thing; it never works completely in that way: Save in the things made
artificially by Man, the workings of centric forces and cosmic are
always flowing together in their effects. In the whole realm of
so-called Nature there is nothing in the proper sense un-living. The
one exception is what Man makes artificially; man-made machines and
mechanical devices.
The truth of this was
profoundly clear to Goethe. In him, it was a Nature-given instinct,
and his whole outlook upon Nature was built upon this basis. Herein
we have the quintessence of the contrast between Goethe and the
modern Scientist as represented by Newton. The scientists of modern
time have only looked in one direction, always observing external
Nature in such a way as to refer all things to centric forces,
— as it were to expunge all that in Nature which cannot be
defined in terms of centric forces and their potentials. Goethe could
not make do with such an outlook. What was called
“Nature” under this influence seemed to him a void
abstraction. There is reality for him only where centric forces and
peripheric or cosmic forces are alike concerned, — where there
is interplay between the two. On this polarity, in the last resort,
his Theory of Colour is also founded, of which we shall be speaking
in more detail in the next few days.
All this, dear
Friends, I have been saying to the end that we may understand how the
relation is even of Man himself to all his study and contemplation of
Nature. — We must be willing to bethink ourselves in this way,
the more so as the time has come at last when the impossibility of
the existing view of Nature is beginning to be felt —
subconsciously, at least. In some respects there is at least a
dawning insight that these things must change. People begin to see
that the old view will serve no longer. No doubt they are still
laughed at when they say so, but the time is not so distant when this
derision too will cease. The time is not so very distant when even
Physics will be such as to enable one to speak in Goethe's sense. Men
will perhaps begin to speak of Colour, for example, more in Goethe's
spirit when another rampart has been shaken, which, though reputed
impregnable, is none the less beginning to be undermined. I mean the
theory of Gravitation. Ideas are now emerging almost every year,
shaking the old Newtonian conceptions about Gravitation, and bearing
witness how impossible it is to make do with these old conceptions,
built as they are on the exclusive mechanism of centric forces.
Today, I think, both
teachers who instruct the young, and altogether those who want to
play an active, helpful part in the development of culture, must seek
a clearer picture of Man's relation to Nature and how it needs to be.
|