Lecture XV
Stuttgart, January 15, 1921
My Dear Friends,
Today I will
deal with some of the things that may be causing you
difficulty in understanding what we have done hitherto. I
will lead over from these difficulties into a realm of ideas
which will show up the inadequacy of those lines of thought
on which the people of our time, with all their comfortable
mental habits, would gladly found their understanding of
universal phenomena.
We have been
studying the universal phenomena in their relation to man. We
have done so in manifold directions. Again and again we have
indicated how a relationship reveals itself between the
forming of man and what appears in the celestial phenomena.
Whether we go by some ancient cosmic system of by the
Copernican theories in forming our pictured synthesis of the
movements of heavenly bodies, we must relate the picture to
man in diverse ways of course, accordingly. This we have
seen. For a true Science we must accept that there is this
relation.
Yet the
difficulties are formidable. Earlier in these lectures we
drew attention to one such difficulty. The moment we try to
form ratios between the periods of revolution of the planets
of our system we come to incommensurable numbers. Arithmetic
runs out, as we might say; we get no farther with it, for
where incommensurable numbers enter in there is no palpable
unit. Thus, when we look for a synthesis of the phenomena of
cosmic space with our accustomed mathematical method and way
of thinking, the phenomena themselves are such that we find
ourselves driven farther and farther from reality. We may not
therefore take for granted that we shall ever be able to
explain the cosmic phenomena on the accustomed basis of our
Geometry, that is to say, within a rigid three-dimensional
space. Nay more, another difficulty has emerged. Yesterday we
found ourselves obliged to assume a certain relationship of
Sun and Moon and Earth, finding expression in some way in man
— in man's very structure. We would fain grasp how the
relation is. Yet if we posit this working-together of the
Three*, we get into formidable difficulties in spatial
calculation.
All these
things we have mentioned. Now we can reach a certain
starting-point at least, through pure Geometry — yet a
Geometry of a higher kind. Thence we may gain an idea of
where the difficulties come from when we are trying by dint
of spatial calculation to grasp the inter-connection of
celestial phenomena. Let us recall our precious attempts to
comprehend the form of man himself. We are then let to this:-
We can and we should try to take seriously that 'memberment'
of the human being of which we have also spoken in these
lectures. The human head-organization, we may truly say,
centring as it does in the nerves-and-senses system, is
relatively independent. So is the rhythmic system with all
that belongs to it. The metabolic system too, and all that
goes with it in the organization three independent systems
are revealed. Taking our start now in an intelligent way from
the principle of metamorphosis, as we must always do when
dealing with organic Nature, we can try to form ideas upon
this question: How are the three members of the three-fold
human system related to each other, according to this
principle of metamorphosis?
Understand me
rightly, my dear friends. We want to gain an idea-though it
be only pictorial to begin with — of how the three members of
the human system are related to each other. On the face of
it, it will of course be difficult. Such organs as are met
with in the human head, it will be difficult to recognise in
them at all clearly the metamorphosis of those organs which
are fundamental to the metabolic and lymph system. But if we
go into the morphology of man deeply enough, we can find our
way. We only have to think most thoroughly along the lines
already indicated. Namely, the essence of the mutual relation
of the long bone to the skull-bone and vice-versa is a
complete turning-inside-out. The inner surface of the bone
becomes the one turned outward. It is the principle by which
you turn a glove inside-out, provided only that the
turning-inside-out involves a simultaneous change in the
inherent relationships of inner forces. If I should turn a
tubular bone or long bone inside-out like a mere glove, I
should again get the form of a tubular bone, needless to say.
But it will not be so if we take our start, as we must do,
from the inherent configuration of the bone. As I described
before, in its inherent configuration the long bone is
oriented inward towards the radial quality that runs right
through it. It is obliged therefore to subject its material
structure and arrangement to the radial principle. When I
have "flipped" it, so that the inner side opens outside, in
its configuration it will no longer follow the radial but the
spheroidal principle. The "inner side", now turned outward
towards the Sphere, will then receive this form
(Fig. 1).

Figure 1
What
was outside before, is now inside, and vice-versa. Take
this into account for the extreme metamorphosis-tubular bone
into skull-bone and you will say: The outermost ends of human
memberment — lymph-system and skull system — represent
opposite poles in man's organization. But we must not think
of "opposite poles" in the mere trivial, linear sense of the
word. In that we go from one pole to the other, we must adopt
the transition which this involves, namely from Radius to
surface of a Sphere. Without the help of such ideas and
mental pictures, intricate as they may seem, it is quite
impossible to gain a just or adequate notion of what the
human body is.
We come now
to what constitutes the middle, in a certain sense, — the
middle member of man's organization. This will be all that
belongs to the rhythmic system, and it will somehow form the
transition from radial structure to spheroidal.
In the
threefold system thus presented we have the key to the
morphological understanding of the entire human organism. Of
course we need to realise how it will be. Suppose we have
some organ in the metabolic system — the liver for example —
or any one of the organs mainly assigned to the metabolism.
(We must qualify it with the word 'mainly' for there is
always an overlapping and interlocking of these things).
Suppose then we begin with such an organ and seek what
answers to it in the head. We try to find which of the organs
in the head-nature of man m ay be connected with it by the
metamorphosis of turning-inside-out. We shall then have to
recognise the organ when entirely transformed, de-formed;
only by so doing shall we understand it. It will therefore
not be easy to take hold of mathematically. Yet without
finding some mathematical way of access we shall never
adequately grasp it. And if you call to mind (even if you
only take this as a picture) — if you call to mind that the
real understanding of the human form and figure will lead us
out among the movements of celestial bodies, you will divine
what must be needful also when we wish to comprehend the
latter. For a true synthesis of the phenomena of movement
among the heavenly bodies, it will be quite inadequate to
think of them as if these movements were accessible to a
Geometry that simply reckons with ordinary rigid space and
therefore cannot master the turning-inside-out. For when we
speak of a turning-inside-out in the way we have been doing,
we can no longer be thinking of ordinary space. Ordinary
space holds good where we can calculate volumes, cubicle
contents in the conventional way. We cannot do so if obliged
to make the inner outer. We can no longer go on calculating
them with the same conceptions which hold good in ordinary
space.
If then in
thinking of the human form and figure I need the
turnings-inside-out, in thinking of the movements of heavenly
bodies I shall need them too. I cannot proceed like the
current Astronomy which tries to comprehend the celestial
phenomena within an ordinary rigid form of space.
Take, to
begin with, simply the head-organization and the metabolic
organization of man. To pass from one to the other you must
imagine, once again, a turning-inside-out — and, what is
more, one that involves variations of form. Let us at least
try to get a picture of the kind of think involved. We did
preliminary work in this direction when speaking of the
Cassini curves, and of the circle differently conceived.
Ordinarily the circle is defined as a curve, all of whose
points are equidistant from one central point. We were
speaking of the circle as a curve, all of whose points are at
measured distances from two fixed points, and so that the
quotient of the two distances is constant. This was our other
conception of the circle.
Speaking of
the Cassini curve, we showed that it has three essential
forms. One, not unlike an ellipse: — this form arose when the
parameters of the curve bore a certain relation, the which we
indicated. The second form was the lemniscate. The third form
is that while in the idea of it — and also analytically — it
is a single entity, to look at it is not. It has two branches
(Fig. 2),

Figure 2
yet
the two branches are one curve. To draw the
line, we should somehow have to go out of space, coming back
into space again when we draw the second branch.
Conceptually, our hand would be drawing a continuous line
when drawing the two regions which look separate. We cannot
draw the line continuously within ordinary space, and yet
conceptually what is here above and what is here below (the
inner curve in Figure 2) is a single line. Now as I also
mentioned, the same curve can be thought of in another way.
You can ask what will be the path of a point which when
illumined from a fixed point A appears with constant
intensity of illumination, seen from another fixed point B.
Answer: a Cassini curve. A curve a Cassini will be the focus
of all points through which a point must run, if when
illumined from a fixed point A it is seen ever with the same
intensity of light from another fixed point B
(Fig. 2 again).
Now it will
not be hard for you to imagine that if something shines from
A to C
(Fig. 2)
and thence by reflection from C to B, the
intensity of light will be the same as if reflected from D
instead. But it gets rather more difficult to imagine when
you come to the Lemniscate. The ordinary geometrical
constructions by the laws of reflection and so on, will not
be quite so easy to carry through. And it gets still more
difficult to imagine with the two-branched curve, that the
same intensity of light should always be observed from the
point B, inside the one branch of the curve, when the
original point-source of light is in A. You would have to
imagine (as you pass from the one branch to the other) that
the ray of light goes out of space and then shines into space
again. You are up against the same difficulty as before, when
you were simply asked to draw the two branches as one — with
a single sweep of the hand through space.
Yet if we do
not develop these conceptions we shall be unequal to the
other task, namely of finding the transmutation — or even the
mere relationship of form — as between any organ in the head
of man and the corresponding organ in the metabolism. To find
the connection you simply must go out of space. Once again —
strange as it may sound — if with your understanding of any
form in the human head you wish to make a transition to the
understanding of a form in the human metabolic system then
you will not be able to remain in space. You must get out of
space. You must get right out of yourself , looking for
something that is not there in space. You will find something
that is as little inside ordinary space as is what intervenes
between the upper and lower branches of a two-branched
Cassini curve. This is in fact only another way of expressing
what was said before that the metamorphosis must be so
conceived as to turn the form completely inside out.
In thinking
thus of the connection between the upper and lower branches
of the discontinuous curve of Cassini (as shown in
Fig. 3)
we are still presupposing actual constants, rigid and unchanged,
in the equation. Now if we vary the constants themselves as
in an earlier lecture, forming equations of twofold
variability, we shall be able to imagine the upper branch
say, in this form and the low one in this
(Fig. 3).

Figure 3
The
upper branch will take this form eventually. If then you
alter the curve of Cassini by taking variables in place of
constants — so that you start with equations instead of
starting with invariable constants — you will get two
different kinds of branches. Then there will also be the
possibility for one of the two branches to come in as it were
from the infinite and go out to the infinite again. This is
precisely the relationship from which you should take your
start when following certain forms within the human head,
comprising them in curves and lines, and then relating them
to the forms of organs or of complexes of organs in the
metabolic system, which in their turn you will comprise in
curves and lines. Such is the intricacy of the human form. To
make it still less simple, you must imagine the one line
(Fig. 3a)
with an outward tendency and the other with its
tendency turned inward.

Figure 3a
You will be
prone to say (I hope without insisting on it, but as a
passing impression): If this be so, the human organization is
so complicated that one would almost prefer to do without
such understanding and fall back on the ordinary philistine
idea of the body, as in the present-day Anatomy and
Physiology. There we are not called upon to make such
prodigious efforts, as to let mental pictures vanish and yet
again not vanish, or turn them inside-out, and all the rest!
May be; but then you never really understand the human form;
your understanding is, at most, illusionary.
Now, to go
on: Suppose you thus look into it and recognize that there is
something in the human organization which falls right out of
space, is not in space at all, but obliges you for instance
to imagine spatially separated line-systems, inherently
united with each other and yet united by another principle
than three dimensional space affords. Thinking in this way,
you will no longer be too far removed from what I shall now
bring forward. You will at least be able to entertain the
thought in a formal sense. No-one, I mean can validly object
to thinking it as a pure form of thought. For to begin with,
all we are called upon to do is to conceive a clear idea, as
in mathematics generally. It cannot be objected that the
thing is unproved, or the like. We are only concerned to
reach a self-contained and consistent idea.
Think
therefore for a moment that you had to do not only with
ordinary space, conceived in its three dimension, but with a
"counter-space" or anti-space". Let me call it so for the
moment, and I will try to evoke an idea of it, as follows.
Suppose I form the thought of ordinary, three-dimensional,
rigid space. I form the first dimension, I form the second
dimension and I form the third dimension
(Fig. 4).

Figure 4
Then
I have, so to speak, filled-in in thought — in the idea
and mental presentation of it — three-dimensional space with
which I am ordinarily confronted. Now as you know, in any
such domain you can not only advance up to a certain degree
of intensity; you can subtract from it too, and as you go on
subtracting — taking away — you come at last to the negation
of ti. As you are well aware, there is not only wealth but
debt. Likewise I cannot only make the three dimensions to
arise in thought but I can also make them vanish. Only I now
imagine the arising and vanishing to be a real process, —
something hat is really there. Of course it is possible to
think only two dimensions instead of three, but that is not
my meaning. What I now mean is this: The reason why I only
have two dimensions
(Fig. 4a)

Figure 4a
is not that I never
had a third. The reason is, I had a third and it has vanished.
The two dimensions are an outcome of the coming-into being and
vanishing-again of the third. I now have a space, which,
though it outwardly shows only two dimensions, must inwardly
be conceived as having two third dimensions, one positive and
the other negative. The negative dimension springs from a
source that can no longer be there in my three-dimensional
space at all. Nor must I think of it as a "fourth dimension"
in the conventional sense. No, I must think of it as being,
to the third dimension, as positive to negative
(Fig. 4a
once more).
And now
suppose that what I have been indicating is really there in
the Universe; yet, as things generally are in the real world,
approximately so. It would then be not a pedantically
accurate but an approximate rendering of what I have here
drawn. This need not cause you any great surprise, for in
outer sense-perceptible reality you never find mathematical
figures reproduced in any other way, always approximately. If
then I claim that the picture represents something real, you
will only expect it to do so in an approximate sense. To
represent a reality corresponding to it, I need not repeat
exactly the same drawing, but I should have to draw something
flattened; that would answer to it. The fact that something
has been there and has then vanished, I may perhaps suggest
in this way: I will suppose that the density of an effect,
indicated by the dark shading, came into being and then
partly faded out again, drew weaker
(Fig. 5).

Figure 5
You are then
left with a sphere that has a denser portion in the middle
region. I beg you know, compare what is here drawn with the
real cosmic system, such as we see it with our eyes, — the
cosmic sphere with all the stars widely dispersed, and then
the stars more densely packed in the region of the Milky Way,
or what we call the Galactic System.
Yet you may
also compare it with something else. Take any popular
star-map. The picture we have shown
(Fig. 5a)

Figure 5a
— let us
still take it simply as a picture — is fundamentally
equivalent to what is always being shown: the passage of the
Sun or of the Earth through the Zodiac, with the with the
North and South poles of the ecliptic somewhere out yonder.
The idea we have been forming is, as you see, not so very
remote from what is there in the outer Universe. In coming
lectures we shall of course still have to look for more
detailed relations.
Now for an
understanding of what was said before about the human being
we have not yet gone for enough. We must go farther and make
the second dimension also vanish; so then we shall be left
with only one, — with a straight line. But this is no
ordinary straight line drawn into three-dimensional space. It
is the line that has remained when we have made the third and
also the second dimension vanish. And now we make the last
remaining one to vanish. Then we are left with a mere point.
Bear in mind however that we have arrived at the point by the
successive vanishing of three dimensions. Now let us suppose
that this point were to present itself to us in reality, — as
having existence in itself. If it is there, and making itself
felt, how then shall we imagine its activity? We cannot
relate its activity to any point in the space determined by
the x-axis. The x-axis is not there, since it has vanished.
Nor can we relate it to anything with an x — and a
y-coordinate, for all of this has gone; all this has vanished
out of space. Nor can we relate it in its activity to the
third dimension of space. What then shall we say? When it
reveals its activity we shall have to relate it to what is
quite outside three-dimensional space. What then shall we
say? When it reveals its activity we shall have to relate it
to what is quite outside three-dimensional space.
Consistently with the procedure we have been through in our
thinking, we cannot possibly relate it to anything that could
still be included in this space. We can only relate it to
what is outside it three-dimensional space altogether. We can
relate it neither to "x deleted" nor to "y deleted" not to "z
deleted", but only to what deletes all three of them, z, y,
and z together, and is therefore into within
three-dimensional space at all.
We put this
forward to begin with as a purely formal, mathematical
notion. Yet is soon grows real. It grows exceedingly real
when we begin to enter into things more deeply than with the
easy-going notions with which Science nowadays would gladly
master them. Look, with this deeper tendency of
understanding, — look at the process of sight and the whole
organisation of the eye. You are perhaps aware (in other
lectures I have often spoken of it) of how the eye is not
merely to be regarded as a thing formed from within the body
outward; for it is largely organized into the body from
outside. You an trace the forming of it from without inward
by studying the phylogenetic development of lower animals and
then considering the act of sight itself. You will contrive
to understand how the process of sight is stimulated from
without and how the organ too is adapted to this stimulation
from without. Then as the process works on inward to the
optic nerve and farther in, it vanishes at length, — vanishes
as it were into the organisation as a whole. I know you can
find the termination of the optic nerves, and yet — this too
comes to expression approximately — if you go into the inner
organisation you will have to admit that it there
vanishes.
So much for
the process of sight and the associated organs. And now
compare with this the process of secretion of the kidneys. Go
into it conscientiously. and you will have to relate the duct
that leads outward, for the secretion of the kidneys, to what
is working from without inward where the eye passes into the
optic nerve. If you then look for ideas whereby the two
things can be related, so that their mutual relation will
help you understand the phenomena of either process, you will
find indispensable such forms of thought as we have just been
indicating. If you conceive the ideas of three-dimensional
space as applying to the process of sight (we might also
replace the one by the other, but if you do it in this
way. ...), then, if you seek what answers to it in the
secretion of the kidneys, you must realize that what is there
enacted takes you right out of three-dimensional space. You
must go through the same procedure in your thinking as I did
just now in extinguishing the spatial dimensions. Otherwise
you will not find your way.
In like
manner you must proceed if you are trying to understand the
curves formed in the Heavens by the apparent paths of Venus
and Mercury on the one hand, Jupiter and Mars on the other, I
mean quite simply the apparent paths as we observe them with
our eyes, — the loops and all. If you use polar coordinates
for example, then for the loop of Venus you may make the
origin of your coordinate system in three-dimensional space.
Here you can do so. But you will not come to terms with
reality if you adopt the same principle when examining the
curve of Mars. In this case you must start from the ideal
premise that the origins of any relevant system of polar
coordinates will be outside three-dimensional space. You are
obliged to take the coordinates in this way. In the former
case you may start from the pole of the coordinate system,
taking coordinates in the normal way, as in Figure 6.

Figure 6
But if
you do this for the one planetary curve — say for the path of
Venus with its loop — you will do equal justice to the paths
of Jupiter or Mars with their loops, only by saying to
yourself: This time I will not pre-suppose a polar-coordinate
system with an origin such that I always have to add a piece
to get the polar-coordinates, as in Figure 6. No, I will take
as origin of my polar-coordinate system the encompassing Sphere
(Fig. 6a),

Figure 6a
i.e. what is there
behind it, indeterminately far. Then I get such coordinates as
these (dotted lines), where in each case, instead of adding, I
must leave so much out. The curve I then obtain also has something
like a centre, but the centre is in the infinite sphere.
It might
prove necessary then, for more profound research into the
paths of the planets, that we make use of this idea: In
constituting the paths of the inner planets we must indeed
attribute to these paths some centre or other within ordinary
space. But if we want to think of centres for the path of
Jupiter, the path of Mars and so on, we must go right outside
this ordinary space.
In fine, we
have to overcome space; we must transcend it . There is no
help for it. If you are conscientious in your efforts to
comprehend the phenomena, the mere ideas of three-dimensional
space will not suffice you. You must envisage the interplay
of two kinds of space. One of them, with the ordinary three
dimensions, may be conceived as issuing radially from a
central point. The other, which is all the time annulling and
extinguishing the first, may not be thought of as issuing
from a point at all. It must be thought of as issuing from
the encompassing Sphere — that is, the Sphere infinitely far
away. While in the former case the "point" is of zero areas
which it turns outward, and a point with the area of an
infinite spherical surface which it turns inward.
Geometrically it may suffice to conceive the notion of a
point abstractly. In the realm of reality it will not. We
shall not do justice to reality with the mere notion of an
abstract point. In every instance we must ask whether the
point we are conceiving has its curvature turned inward or
outward; its field of influence will be according to
this.
But you must
think still farther, my dear friends; there is a another
thing. Of course you may imagine that you had somewhere
caught this point which is really a Sphere. To begin with,
since it is in the infinite far spaces you need not imagine
it just here
(s, Fig. 7).
You can equally well imagine it a
little farther out, (b, or c). You can imagine it to be
anywhere out there; you only have to leave this sphere free
(strongly drawn sphere in Fig. 7).
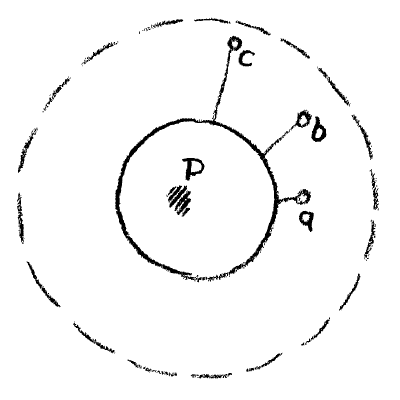
Figure 7
For this is hollowed
out, so to speak; this is the inverted circle or the inverted
sphere, if you like. But now suppose the following might be
the case. Think of what is within this peculiar circle
(namely at a, b, c, etc,) Think of this point that has its
curvature turned inward. For in effect, the entire space
outside this spherical surface is then a point with its
curvature turned inward. And now imagine that this space had,
after all, its limit somewhere. You might be able to go far
away out, — very far. Suppose however the reality were such
that you could not just go anywhere, but somewhere after all
there was a limit of quite another kind (dotted circle in
Figure7). What there would appear, as if by inner necessity,
what in effect belongs to the realm beyond the limit. An
equivalent sphere would have to arise within, belonging to
what is there outside. You would then have to realize: Out
there, beyond a certain sphere, something is still existing,
it is true, but if I want to see it I must look in here (P),
for here it re-appears. The continuation of what is faraway
out there make itself felt in here. What I am looking for as
I go out into infinite distances, makes its appearance
within, and becomes manifest to me from this centre.
These are the
kind of ideas you should develop to an adequate extent. In a
formal sense they look sound enough. As forms of thought
there can surely be no objection to them. Truly remarkable
results will be obtained however, if with their help you try
to penetrate outer reality. Think for example that there
might be a phenomenon in celestial space, — we may call it
"Moon" to begin with, — yet this phenomenon were not to be
understood simply by saying: "This Moon is a body, here is
its central point; we will investigate it on the
understanding that it is a body and that its central point is
here." Assume (and please forgive my saying, I put it
euphemistically) assume that this way of thinking did not fit
the reality, but that I ought to express it quite
differently. I ought rather to say: "If I, in my Universe,
start from a certain point and go farther and farther out, I
come at length to where I shall no longer find heavenly
bodies. Yet neither shall I find a mere empty Euclidean
space. No, I shall find something, the inherent reality of
which obliges me to recognize the continuation of it here (at
P)." I should then be obliged to conceive the space contained
within the Moon as a portion of the entire Universe with the
exception of all that exists by way of stars, etc., outside
the Moon. I should have to think on the one hand of all the
stars here are in cosmic space. These, I am now assuming I
have to treat in one way, according to a single principle;
but the inside of the Moon — the space contained within the
Moon — could not be treated in this way. It would require me
to think as follows: There on the one hand I go out into the
far spaces. Somewhere out there, I presume, is the celestial
Sphere. Though it be only the "apparent" Sphere to begin
with; something effective, something real must be conceived
to underlie it. Yet whatsoever realities I find out there,
the space within the spherical surface of the Moon has
nothing whatever to do with it. It only has to do with what
begins where the stars come to an end. It is a fragment, in
some strange way, belonging not to my Universe but to that
Universe to which all the stars do not belong.
If there is
such a thing within a Universe, it is a thing inserted in
this Universe, occluded as it were, — thing of altogether
different nature and revealing different inner properties
from all that is there around it. And we may then compare the
relation of such Moon to its surrounding Heavens with the
relation which obtains for instance between the secretions of
the kidneys — with the organic structure that underlies them
— and on the other hand the structure and functioning of the
eyes. From this we shall proceed tomorrow.
It is not due
to me that I must try to form, and to acquaint you with, such
complicated notions of how the Universe is built. Truth is,
equipped with any other notions you will not make headway,
save on the convention: "Let us comprise the phenomena with
our given range of ideas, and if we come to a limit
somewhere, well then we do, and we go no further". Ascribe it
then to the reality and not to any craving for remote ideas,
if in the effort to impart an understanding of how the
Universe is built I have unfolded complicated notions.
|