LECTURE VIII
Dornach, April 23, 1921
Today, I
shall have to turn to a seemingly more remote topic that will
fit in, however, with yesterday's and tomorrow's subjects. I
have frequently mentioned that when the evolution of humanity
is surveyed, people proceed too much from the premise that
the general condition of human soul life has basically
remained the same ever since any human development can be
traced historically or in prehistory. However, this
assumption simply does not correspond to the facts. It is
difficult, of course, to ascertain what the successive
metamorphoses of human soul evolution were like if one is
merely in a position to study the facts recorded in
historical documents. If, on the other hand, one is able to
look back further than these facts allow, then even the
historical traditions present themselves in a different
light. It then becomes evident that the human soul condition
was not always what it is today or what it was in the ages
still discernible by external means.
Above all,
people believe the following: Human beings utilize something
like geometry, like arithmetic, which, as we know, is mainly
the theory of counting. Furthermore, they master the art of
weighing, of determining weights of given objects. People
then consider what measuring and measures represent and
contemplate the way one counts and weighs things today. Then
people think: Surely, in the age when, according to modern,
prevalent opinion, human beings were still completely
childlike, they were incapable of measuring, counting, and
calculating anything. But ever since human beings were
capable of that, these matters have been carried out
approximately in the same way we execute them nowadays.
This is not
the case at all, and even though it will lead us into a more
remote subject, as I said, we must acquire a more exact idea
of measures, numbers, and weights before we go into the
historical considerations about mankind. Even according to
external historical tradition the views concerning numbers
prevailing in the Pythagorean School differed somewhat from
those of today. As all of you realize, the Pythagoreans
connected certain ideas with the numbers one, two, three,
four, and so no. They linked quite definite conceptions with
an even and an odd number. In short, they spoke about numbers
in a certain qualitative sense, not merely in a quantitative
one.
When the
underlying reason for this is considered from the standpoint
of spiritual science, we arrive at the realization that the
Pythagorean School, which as yet was still a kind of esoteric
school, represented basically only the last vestige of a much
more ancient wisdom of numbers, going back to primordial
times of which only the traditions have been preserved. And
what is handed down to us concerning a science of numbers by
Pythagoras is in fact already a decline from a much older
teaching of numbers. When these matters are pursued further
with the methods of spiritual science, we arrive by way of
measure, number, and weight at concepts essentially different
from those we possess today. As I said, even though it might
create difficulties for some of you, we must make it somewhat
clear to ourselves how these concepts of measuring, counting,
and weighing are constituted today.
Measuring
— how do we measure? We can only have one
measure and it must be assumed in some manner. We cannot claim
that this measure on which we base everything, such as the
metric measure today, is somehow determined absolutely. It is
determined as a certain segment of the northern quadrant of
the earth's meridian that passes through Paris, and this
segment, the ten millionth part, is not even exactly
contained in that original prototype meter located in Paris.
It is assumed, however, and we say that we proceed from a
certain measure. With it, we then measure other lengths or
surface areas by forming a square measure out of the unit of
length. Yet, the figures arrived at concerning the object
being measured refer to something completely arbitrary that
was at one time assumed. It is important to make it clear to
ourselves that we actually take an arbitrary measure as the
basis, hence, that we always arrive only at a relation of
some object to this arbitrarily assumed measure when we
measure an object.
It is
somewhat different in the case of numbers. In the abstract
manner of our life today, we count, 1, 2, 3; we do
this when counting apples or people, horses or chairs. To the
object that is to be determined by the number it matters not
what we designate as 1. We apply our peculiar way of
counting to all things we count off, which, as a unit,
represent an integrated totality.
Please note
that in measuring we proceed from an arbitrary measure and we
then relate everything to this arbitrary unit of measure.
This unit of measure is something, so to speak; it exists. It
is even conceivable, as it were, almost like a thing, an
object. The unit of numbers cannot be pictured in this way.
The unit of number is a completely abstract concept
applicable to anything. No matter whether we count years or
people or stars, we are led into total abstraction, into
something that cannot stand for any particular reality since
it could stand for all realities. When we take the arithmetic
unit as the basis, the minute objective element still
retained in measuring is lost to us.
When weighing
something, we do not see the whole extent of what we take as
the basis of weighing. There, the whole matter escapes us
even more than in the case of numbers. When we count chairs,
for example, and we say, “one,”
“two,” “three,” we are at least
finished when we come to the third chair that stands before
us as a unit. In the case of a scale, on the other hand, we
place a weight on one side of the scales — a weight in
itself is nothing if it is not subject to earth's gravity, as
we say — and the object we weigh is equal to the weight
of the weights. Here, however, we are no longer by ourselves;
basically, the whole earth is involved. Our point of
reference here lies somehow completely beyond the realm we
oversee. We enter into a complete abstraction when we say
that something weighs five kilograms. Just think what you
actually picture when you say that something weighs five
kilograms. You place a five kilogram weight on a scale, but
this weight by itself is really nothing! We are not dealing
with a property of the thing itself. When I say, “one
chair,” this one is at least integrated in the
chair. The five kilograms, on the other hand, must relate
themselves to the earth. You merely deal with something that
relates to something else the whole extent of which you do
not see at all, namely, the whole body of the earth. And when
weighing the other object on the scale, which is to weigh
five kilograms, again, you have something that escapes you
completely, belonging again to a totality that is even less
than an abstraction.
Let us
proceed from numbers. In former times, and here we actually
go back as far as the second post-Atlantean epoch, all
thinking concerning numbers was dealt with in a significantly
different manner from the way we treat it today in the
outside world. People then really had concepts of 1,
2, and 3. For us, 2 is nothing but
the presence of two units of 1; 3 is the
presence of three, 4 that of four units of
1. Thus we continue counting by always adding 1
more. hence repeating the same act of thinking. We can repeat
it indefinitely.
This was not
the case in the second post-Atlantean epoch. Back then,
people sensed the same difference between, let's say,
two and three that we today feel only
between different objects. In the number 3, one
sensed a significantly different element from that in the
number 2. Not only was it the addition of one unit; rather,
one sensed something integrated in the 3, something
where three things relate to one another. The 2 had
an open element, something where two things lie indifferently
side by side. People recalled this indifference in lying side
by side when they said “two.” They did not sense
this in the number 3, but only something that belongs
together, where each thing relates to all the others.
Concerning 2, a person could imagine that one thing
escapes to the left, the other to the right. The 3 could not
be pictured that way; instead, it was felt that if one unit
would disappear, the remaining two would no longer be what
they had been, for then, they would exist indifferently
beside each other. The 3 combined the 2 in
a totality, so to speak; it made them a whole. The form of
arithmetic we have today, our elementary counting, this
repetition of the same act, did not exist at all in those
former times. Only now, through spiritual science, we are
once again directed in a certain sense to the qualitative
element of numbers.
I can
illustrate this with an example long since familiar to you so
that you will realize that it is necessary to add not only 1
to 1, and so on, but to delve into the reality of existence
with the numbers. In order to give you at least a very
elementary idea of this matter, let me outline the following.
In my book,
Theosophy,
[Note 1]
the individual members of the human being are described:
1. Physical Body
2. Ether Body
3. Astral Body
4. Sentient Soul
5. Intellectual or Mind Soul
6. Consciousness Soul
7. Spirit Self
8. Life Spirit
9. Spirit Man
To list the
members of the human being side by side like this, however,
signifies counting them off abstractly one after the other;
it means that we do not delve into reality. Because these
nine do not exist, we cannot count them like that at all:
“1. physical body, 2. ether body, 3. astral body, 4.
sentient soul.” You cannot count like that when you
wish to comprehend the human organization and observe human
beings today in their reality. In fact, it must be put like
this: The physical body is delimited as an integrated whole,
so is the etheric body. Pass on to the third member, on the
other hand, it is not something self-enclosed. In the case of
the actual human being, we cannot just add the sentient soul
to the astral body. Instead, these two, the astral body and
the sentient soul, must definitely be combined and thereby,
passing from one to two to three
in reality, we can, as it were, count off realistically, not
merely finding in the 3 the simple addition of
1.
What develops
in us as the “astral body” and the
“sentient soul,” which interact with each other,
is simply a third element, abstractly speaking, but by
passing in reality to this third element, a third unit can no
longer merely be added to the first two. Instead, we must
realize that this third element is in itself different from
the first two.
Then, the
fourth member is counted off, which is actually the fifth,
and again, in the modern human being, we must basically add
together the sixth and seventh. Thus, we arrive at the way
they are actually listed in my
Theosophy:
3, 4, 5,
6, 7. We have seven actual components, which, when they are
abstractly counted off, are nine:

Based on
reality, we learn to say: By proceeding according to their
inherent rules, one thing is not indifferent to the others.
Just because this is the third member (see above, 3), it is
something different. Certainly, due to our customary abstract
thinking about numbers, we have to illustrate this a little,
for this older way of thinking about numbers is foreign to
ordinary consciousness. In ancient times, on the other hand,
in the first and second period of the post-Atlantean epoch,
it would not have occurred to anybody to imagine an
indifferent addition in progressing from one number to the
next. Instead, people experienced something when they passed
from, say, 2 to 3, just as we experience something here when
we pass from 2 to 3 (see above list). Today you can barely
sense it in this example, but not yet in the number itself.
In those former times people could sense it in the numbers
themselves. They spoke of numbers in reference to their
mutual relationships. Anything that existed in twos, for
example, was felt to have a quality of openness towards the
world, of not being closed off. Something existing in threes,
as an actual three, was something closed off. You might now
say that depending on what is counted a distinction has to be
made. When you count, one man, one woman, one child, man and
woman are equal to a duality, hence not closed off to the
world; the child closes this duality off, forms a totality.
When you count apples, on the other hand, we can indeed not
say that three apples are more closed off than two. It was
true that external matters were merely sensed in this way,
but the number itself was experienced quite differently.
You might
recall that certain aboriginal tribes still use their ten
fingers to count, comparing to them the amount of objects
present in their surroundings. So we could say that if we
have three apples here, this is equal to three fingers.
For 1, 2, 3,
however, these primitive people would not have said —
naturally in the words of their own language —
“thumb,” “index finger,” and
“middle finger.” Although the objects they
counted off in the outside world remained undefined, what
represented those objects inwardly was very clearly defined,
for the three fingers differ from one another. Well, mankind
has now advanced so splendidly in the fifth period of the
post-Atlantean epoch — basically, it was already like
this in the fourth period — that we no longer need to
count by means of our fingers. Instead, we say, “one,
two, three.” The genius of language is not taken into
consideration anymore. For if you would listen to what is
contained in the words, purely based on feeling you would
say: “Eins, entzwei” (“one, in two
— cut in two.”)
(Translator's Note 1)
It is still retained in the language, and when
you say: “Drei” (“three”), and you
are sensitive to the sounds, you have something closed off.
Three: when pictured correctly, three things can only be
imagined as lying in a circle, connected to each other; two:
into two (entzwei); three: self-enclosed, the genius
of language still retains that.

Well, as I
said, we have “advanced so far” that we can
abstractly add one unit to another. Then we feel that this is
2, that is 1; in case of 3, one
more has been added, and so on. Yet, why is it that we can
count in the first place? In reality, we don't accomplish it
any differently from primitive peoples. Only they did it with
their five physical fingers. We, too, count with the fingers,
but with those of our etheric body, and we no longer know it.
It takes place in our subconscious, and we leave that out of
consideration. We actually count by means of the etheric
body; in reality, a number is still nothing but a comparison
with what is contained within us. The whole of arithmetic is
in us; we brought it to birth within us through our astral
body. It actually emerges from our astral body, our ten
fingers being merely replicas of the astral and etheric.
These two are only utilized by the external finger, whereas,
when we do sums, we express in the etheric body what brings
about the inspiration of numbers in the astral body; then we
count by means of the etheric body, with which we think in
the first place.
Therefore, we
can say that, outwardly, counting is something quite abstract
for us today; inwardly, the reason we count is connected with
the fact that we are counted in the first place, for
we are counted out of universal being and are structured
according to numbers. It is most interesting to trace the
various methods of counting among the different folk groups
in the world — according to the number 10, the decimal
system, or the number 12 — and how this relates to
their different etheric and astral constitutions. Numbers are
inborn into us, woven into us out of the cosmic totality.
Outwardly, numbers are gradually becoming a matter of
indifference to us; within us, this is not the case. Within
ourselves, each number has its own definite quality. Just try
and imagine that you could eliminate numbers from the
universe and then see what things formed in numbers would
look like if one thing were merely added to the other.
Imagine the appearance of your hand, if the thumb were here,
and the next finger would be added as the same unit and then
the next, and so on. You would have five thumbs on your hand
and five on the other! This would then correspond to abstract
counting.
The spirits
of the universe do not count like that. They create forms
according to numbers, and they do it in the manner formerly
connected with numbers during the first and even the second
period of the post-Atlantean epoch. The development of
abstract numbers out of the quite concrete concept of the
element and quality of numbers is something that only evolved
in the course of humanity's evolution. We have to realize
that it has profound significance that the tradition handed
down to us from the ancient mysteries relates that the gods
fashioned man according to numbers. The saying that the world
abounds in numbers implies that everything is fashioned
according to numbers and that the human being, too, is formed
on the basis of numbers. Hence, the modern way of counting
did not exist in those ancient times; on the other hand, an
imaginative thinking in the qualities of numbers did
exist.
As I said,
this leads us back to an age of long ago, namely, the first
and second post-Atlantean periods, the ancient Indian and
Persian eras, in which our present form of counting was not
at all possible. In those times people connected something
entirely different from two times one with the number 2. And
likewise they associated something other than two plus one
with three. As you can see, the human soul constitution has
indeed changed considerably in the course of time.
Turning now
to the somewhat later period of time, the third period of the
post-Atlantean epoch, we find that the measure was something
quite different. Today, we measure on the basis of an assumed
and arbitrary unit of measurement. Even in the third
post-Atlantean period, for example, people did not really
refer to such an arbitrary unit of measure. In measuring,
they had in mind something quite pictorial. What they focused
on may perhaps become clear to you from the following. Here,
for instance, we see one column, there is another one (see
sketch below); we look at these two columns. If we experience
things abstractly, we say that the second column is twice as
high as the first one; we measure it by the first one.

That,
however, is a very abstract conception. Picturing it
concretely, we can interpret it in approximately the
following manner: When we evoke a feeling for the column on
the left, we experience it to be weak in comparison to the
one on the right. We feel that it must grow, and when it
grows and grows and reaches this point up here (pointing to
the taller column), it has become something special. It has
put so much energy into this growth that it now possesses a
strength such that its two parts are both equally strong. You
can sense something qualitative there. You can go further and
say: I have a structure here; I measure it against the other
one and thus arrive at the symmetry; the concept of the
measure expands for me, entering into the picture.
In this way,
we gradually come to the idea that measure actually has to do
with something that is still sensed dimly when we speak of
moderation
(Translator's Note 2)
in which case we are not thinking of measuring something. For
example, when a person consumes only a certain quantity of
some food, we might designate that as being moderate
(maessig) without having measured the amount. We
classify something else as immoderate (unmaessig).
We are not measuring anything here, we make no comparison,
measuring the stomach with what enters it, and so on. We
don't measure the piece of meat and then eat it; we do not
measure it against the size of the person. Instead, we refer
to a quality when we speak of a moderate or immoderate intake
of food. We arrive at something that is not so very different
from what we term a measure today but it does show us that we
refer to something abstract today when we speak of
measure, namely, “the unit of measure
contained in a certain quantity,” whereas formerly
people defined it as something that was qualitatively
connected with objects.
Above all,
people sensed the measured symmetry of each member of man in
relation to the totality of the human being without thinking
at that point of a unit. One thing has remained from this,
namely, that it seems abhorrent to us if, as artists, we are
supposed to measure anything; for, if an artist actually has
to take measurements so that the nose, for example, does not
turn out to be too long or too short, this is not considered
artistic. But we consider the work artistic when we see that
the thing has the proper size for an organism. Therefore, we
do not deal with an abstract process here but with something
related to the pictorial element.
Finally,
consider the unit of measure that still plays a certain role
today, namely the so-called golden mean or golden section. It
is not connected with measurements but only with a
qualitative element. The smaller element is to the
medium-sized one as the medium-sized one is to the whole. The
smaller element may be any size, but it must always be to the
medium-sized one as the medium-sized one is to the whole. We
do not have a measurement in mind but something that reveals
a certain interrelationship when we look at it. Yet, we speak
of the harmonious measure that comes to expression in the
golden mean. We cannot base the golden mean on any kind of
unit of measure in the abstract sense as we do otherwise.
Therefore, as we examine the various periods of humanity's
evolution in regard to measuring, we find that in the fourth
post-Atlantean period, the Greco-Roman age, this vivid
awareness of measure and symmetry gradually transformed
itself into abstract measuring. This was actually not the
case until the fourth post-Atlantean period. In the third
period people experienced the relationships of measure, the
proportions, much more the way we only experience the golden
mean. Likewise, as we go back into ancient times, our
abstract counting can be traced back to an experience of the
inner quality of numbers.
In the case
of weight, human beings are already far removed from what
existed in the first post-Atlantean period as an experience
of weight. You need only recall a well-known phenomenon that
most of you have experienced in observing an athlete who
lifts a heavy weight with the inscription, “200
kilograms”; he tries and tries to lift it, sweating all
the while, and you almost perspire with him. Then, when he's
let you sweat long enough, he suddenly lifts it up and
carries it off. The whole thing really has no absolute
weight; that has only been feigned. You feel the weight
because of the abstract inscription “200
kilograms.” The experience of weight is something we
are deprived of nowadays. Therefore, it is one of the most
profound experiences when, in regard to natural phenomena,
the experience of absolute weight appears in clairvoyant
consciousness, as is indeed the case.
It is really
true that in the first post-Atlantean epoch, designated as
the ancient Indian epoch, a human being still experienced
something of weight relationships within himself. I have
pointed out many times that our brain actually floats in the
cerebral fluid and therefore — according to the well
known law whereby a floating body seemingly becomes lighter
by the amount of the weight of water it displaces —
loses a considerable amount of its weight. Otherwise, the
brain would crush the blood vessels lying underneath. The
brain floats in the cerebral fluid, but people in their
abstract awareness no longer notice this today; neither are
they aware of any other relationships within themselves. We
no longer experience weight, pay it no attention. There is a
major difference between experiencing one's weight at age
twelve, and when one is, say five times that age. Most people
have forgotten, however, how heavy they appeared to
themselves at age twelve, and therefore they cannot very well
make the comparison. But let's assume that according to the
scales you have the same weight at two ages. Yet this does
not matter; what matters is the experience of the weight.
This experience of weight that for people today is present
only in regard to the earth, was something absolute during
the first postAtlantean epoch.
Today, we
experience only a remnant of that in art but there in a very
pronounced manner. I need only call your attention to the
following. Let us assume that I draw two figures. According
to my view, this is really something unclear and unresolved,
something that should not be. Two objects like that side by
side induce me to draw a third one. But I can shape the third
object only in such a way that it appears larger, in a sense,
holding the other two together. Then I have the feeling that
the three are floating in air and can mutually support each
other.

When a
painter nowadays draws three angels who are, after all, not
viewed in connection with gravity, and he is concerned with
composition, he distributes them in space in such a manner
that they support each other, that one is borne by the other.
Artistically, it would be the worst thing simply to draw
three angels side by side on a canvas; such a painter would
have no true artistic feeling. One must have a feeling for
the weight of each one, how one thing carries the other. In
artistic feelings, a slight touch has remained of what was
mainly experienced inwardly by people in the post-Atlantean
age as producing weight, as giving him weight.
The
experience of weight, number, and measure developed during
the first three post-Atlantean periods according to the way
human beings experienced themselves within the cosmos. And
based on what had shaped them from out of the cosmos, the
other matters were judged, namely, what they produced. When
people observed what their astral body pushed into the
etheric body, they had to tell themselves that the astral
body counts, counts in a differentiating way thus forming the
etheric body. Numbers are found between astral and etheric
body and they are something alive and active within us.
Something
else is located between etheric body and physical body.
Through the inner relationships something is formed out of
the etheric body that we can then behold. Basically, even our
organism is structured according to the golden mean: the
forehead is to a certain other part of the head as that in
turn is to the whole length of the head, and so on. All this
is imprinted by the etheric body into our physical body out
of the cosmos and its relationships. Contained within us,
measure and symmetry represent the transition from the
etheric to the physical body. Finally, in the transition from
the ego to the astral body lives what can be inwardly
experienced as weight. I have often pointed out that the ego
was actually born in the course of human evolution. The
people of the ancient Indian period did not yet experience
such an ego. They did, however, experience within themselves
something causing weight, the condition of possessing form;
hence, they sensed this heaviness, this downward pull, as
well as their buoyancy, their ascent. They sensed within
themselves what is overcome when the child changes from a
being that crawls on all fours to one that walks. The people
in ancient India did not experience their ego, but they did
sense that they were fettered by the Ahrimanic forces to the
earth, that they were weighted down by them, and that, on the
other hand, they were borne upwards, lifted up by the
Luciferic forces. All this, they experienced as their
position of equilibrium. If we were to study the ancient
terms for the ego we would find that the above experience was
contained in the formulation of the words themselves. Just as
the words were fitted together in the verbs according to
their inner configuration, so the ancient words for the ego
contained the balance between floating and falling.
|
I
|
—
|
Astral Body
|
—
|
Etheric Body
|
—
|
Physical Body
|
|
|
Weight
|
|
Number
|
|
Measure
|
|
Weight, which
isn't abstract anymore, for we confront something completely
unknown; number, something quite abstract, for it is totally
unrelated to what is being counted; measure, which has become
increasingly abstract for us — these abstract conceptions
of ours are actually projected from our inner being to the
outside. Something that has very real significance within the
human being since he is fashioned according to measure,
number, and weight is transferred by him to the indifferent
external things. In this process of abstraction the human
being dehumanizes himself. It is therefore possible to say
that mankind's evolution tends in the direction of losing the
inner experiences of weight, number, and measure, retaining
only a slight touch of them in the artistic realm. We no
longer experience them in such a manner that we sense
ourselves as having been formed out of the cosmos according
to weight, number, and measure.
The geometry
we have when we compare congruent and similar figures, when
we say that an ellipse is generated by a point so moving that
its distance from a fixed point divided by its distance from
a fixed line is a positive constant, is something abstract.
There, we basically measure the distances and find that their
sum is always equal to the large axis of the ellipse. Even if
it was not pictured in any way, the ellipse was nevertheless
experienced by people in the third post-Atlantean period in
this peculiar relationship of two different quantities. In
the relationship of one to the other they already sensed the
elliptic element, just as they sensed the circle during the
same age. And in the same way the nature of numbers was
experienced. Humanity evolved in this way from concrete
experience to something abstract, developing geometry out of
the ancient experience of measure, arithmetic out of the
former experience of numbers, and having completely lost the
ancient experience of weight and thus having utterly
dehumanized themselves, human beings developed only external
observation out of it.
All this
slowly prepared the way for the increasing abstractness of
inner human experience, a development that culminated in the
nineteenth century. Thus, the human being became lost to his
own conception. He can no longer comprehend himself; he no
longer has any idea that he produces geometry because
he has been formed according to measure out of the
cosmos, that he counts through his very nature. He is
surprised when the so-called savages use their fingers in
order to compare external objects with them. He has forgotten
that he has been fashioned according to numbers out of the
cosmos. He does not know that in this regard he, too, always
remains a “savage,” that his etheric body had
imprinted the numbers into his astral body in accordance with
the inner qualities of the numbers themselves so that he
could later experience the numbers also outside himself. In
the course of humanity's evolution, geometry, arithmetic, and
the science of weight and weighing have all moved into the
abstract domain and have contributed to the fact that the
human being could henceforth only devote himself to a science
and a form of scientific research that observes these matters
externally.
What do we do
when we are involved in scientific research today? We
measure, count, and weigh. Nowadays, you can indeed read of
strange definitions of existence. We already have thinkers
who state that existence, being, is that which is measurable.
Yet, they naturally refer only to measuring with an arbitrary
unit of measure. It is odd that existence is traced back to
something actually based on arbitrariness. Therefore, the
human being dwells in something that has been completely
detached, excluded from him and in regard to which he has
utterly lost the connection with himself. Due to such
influences, the human being has lost himself in modern
knowledge; something I have emphasized from a number of
viewpoints, particularly during this lecture course.
As I have
often said, the human being has been lost in our perception
of ourselves as merely the last step in the evolution of the
animals. In society we have lost sight of the human being,
for though we have invented extremely sophisticated machines,
we are unable to integrate the significance of the people
operating these machines into our social processes. We must
learn to penetrate mankind's evolution; above all we must
observe in this way how the process of man's
intellectualization has come about. Just think how different
people's frame of mind was in the first post-Atlantean period
when they continuously experienced a changing equilibrium in
placing one leg in front of the other. They always felt
themselves become heavy, sensed a falling and floating.
Picture how different it was when human beings felt that
numbers permeate their own form, that they are built up
according to measures. Think of how different that was from
superficial measuring, counting, and weighing, leaving out
the human being altogether. As I already indicated, at most
it is possible for a person with a more sensitive awareness
for language to gain some insight into the nature of numbers
by means of what is in fact contained in the numerals, the
words naming the numbers; or, from an artistic viewpoint, it
is possible to sense that this, for example, in the sketch
below is feasible:
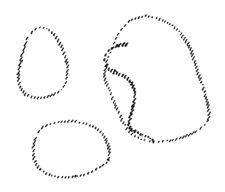
but that this is impossible in this connection:

Such a person
then has just a touch of the feeling for the inner condition
of weight, the inner balance. If, by means of a line, I can
follow some relationship in the other object, I have them
balancing each other. However, if I sketch a protrusion over
here, on the object on the right of second sketch, where
there cannot be one, then I have no feeling for this balance.
See how mankind has struggled to produce the external
proportions out of its inner being, so to say, the outer
appearance in contrast to the inward experience. Take a look
at the painting by Raphael — it is actually true of all
of Raphael's paintings but especially obvious in this one
— depicting the
“Marriage of Mary and Joseph,”
[Note 2]
and see how the figures are positioned and painted in such a
way that they support each other and that the viewer thus loses
the feeling that anything exerts a downward pull. In particular,
however, when ancient painters drew some flying creature,
study how that was motivated, how you can clearly discern
from this figure that it is not pulled down by weight but,
rather, supports itself somehow by means of the relationship
to other elements in the painting.
So, here we
have the transition from the experience of the inner
weighting to the external determination of weight: thus, here
we have the course of mankind in the post-Atlantean epoch
from inward experience to intellectualism, this struggling
ascent to the intellect where everything experienced in our
concepts is divorced from the human being; where we no longer
experience the tearing in the word entzweien,
(“to fall out with each other”; literally:
“tearing in two”) when we say Zwei
(“two”).
All this
comes about slowly. When this term is employed further, when
we say, zweifeln, “to doubt,” we sense the
derivation from entzweien. After all, one who doubts
something implies: Perhaps this is correct, perhaps it is
not. It is open in both directions, the feeling of entzweien
is inherent in the conceptual act. It is also already
contained in the word for the number 2,
zwei. Three — there you cannot experience this
in the same manner when you apply it to something. Apply it
to a judgment, where you have the major premise, the minor
premise and the conclusion: a triad, a matter enclosed within
itself. Take the syllogism about the most famous logical
personality, the one about Gaius Julius Caesar:
All men are mortal;
Gaius is a man;
therefore Gaius is mortal
It all
belongs together, the major and minor premise and the
conclusion. However, if you take merely the first two, the
matter remains open.
Hereby, I only wished to indicate to you what mankind's path
to abstraction was like and how, in fact, by losing himself,
man brought the intellect into his evolution.
We shall continue with this tomorrow. Today's subject was
intended only as an episode, but you will see how it will fit
in with further considerations.
Translators Notes:
1. Translator's note:
In the original German, Rudolf Steiner's example is quite
clear. This is the reason the German words were retained
and the English translation given in parenthesis.
2. Translator's note:
In German, this example is immediately clear. Mass means
“measure;” maessig and massvoll mean
“moderate.”
|