Lecture XIII
Stuttgart, January 13, 1921
My Dear Friends,
In popular
works, as you are well aware, the evolution of astronomical
ideas is thus presented — Until Copernicus, they say
the Ptolemaic system was prevailing. Then through the work of
Copernicus the system we accept — though with
modifications — to this day, became the intellectual
property of the civilised world. Now for the thoughts we
shall pursue in the next few days it will be most important
for us to be aware of a certain fact in this connection. I
will present it simply by reading, to begin with, a passage
from Archimedes. Archimedes describes the cosmic
system or starry system as conceived by Aristarchus of
Samos, in these words — “In Aristarchus'
opinion the Universe is far, far greater. He takes the stars
and the Sun to be immobile, with the Earth moving around the
Sun as centre. He then assumes that the sphere of the fixed
stars, — its centre likewise in the Sun, — is so
immense that the circumference of the circle, described by
the Earth in her movement, is to the distance of the fixed
stars as is the centre of a sphere to the surface
thereof.”
Taking these
words to be a true description of the spatial
World-conception of Aristarchus of Samos, you will admit:
Between his spatial picture of the Universe and ours,
developed since the time of Copernicus, there is no
difference at all. Aristarchus lived in the third Century
before the Christian era. We must therefore assume that among
those who like Aristarchus himself were leaders of cultural
and spiritual life in a certain region at that time,
fundamentally the same spatial conception of the World held
good as in the Astronomy of today. Is it not all the more
remarkable that in the prevailing consciousness of men who
pondered on such things at all, this work-conception —
heliocentric, as we may call it, — thereafter vanished
and was supplanted by that of Ptolemy? Till, with the rise of
the new epoch in civilisation, known to us as the Fifth
post-Atlantean, the heliocentric idea comes forth again,
which we have found prevailing among such men as Aristarchus
in the 3rd Century B.C.!
(For you will readily believe that
what held good for Aristarchus, held good for many people of
this time.) Moreover if you are able to study the evolution
of mankind's spiritual outlook — though it is difficult
to prove by outer documents — you will find this
heliocentric conception of the World the more widely
recognised by those who counted in such matters, the farther
you go back from Aristarchus into more distant times. Go back
into the Epoch we are wont to call the Third post-Atlantean,
and it is true to say that among those who were the
recognised authorities the heliocentric conception prevailed
during the Epoch. The same conception prevailed which
Plutarch says was held by Aristarchus of Samos. Plutarch
moreover described in such terms that we can scarcely
distinguish it from that of our own time.
This is the
noteworthy fact. The heliocentric conception of the World is
there in human thought, the Ptolemaic system supplants it,
and in the Fifth post-Atlantean Epoch it is re-conquered. In
all essentials we may aver that the Ptolemaic system held
good for the Fourth post-Atlantean Epoch and for that alone.
Not without reason do I bring this in today, after speaking
yesterday of an ‘ideal point’ in the evolution of
the Kingdoms of Nature. As we shall see in due course, there
is an organic relationship between these diverse facts. But
we must first enter more fully into the one adduced
today.
What is the
essence of the Ptolemaic cosmic system? The essence of it is
that Ptolemy and his followers go back again to the idea of
an Earth at rest, with the fixed-star Heavens moving around
the Earth; likewise the Sun moving around the Earth. For the
movement of the planets, the apparent forms of which we have
been studying, he propounds peculiar mathematical formulae.
In the main, he thinks in this way: Let this be the Earth
(Fig. 1).
Around it he conceives the
Heaven of fixed stars. Then he imagines the Sun to be moving
in an eccentric circle round the Earth. The planets also move
in circles. But he does not imagine them to move like the Sun
in one circle only. No; he assumes a point
(Fig. 1)
moving in this eccentric circle which he
calls the ‘Deferent’, and he makes this point in
its turn the centre of another circle. Upon this other circle
he lets the planet move, so that the true path of the
planet's movement arises from the interplay of movements
along the one circle and the other. Take Venus for example.
Says Ptolemy: around this circle another circle is rotating;
the centre of the latter circle moves along the former. The
actual path of Venus would then be, as we should say, a
resultant of the two movements. Such is the planet's movement
around the Earth; to comprehend it we must assume the two
circles, the large one, called the “deferent”,
and the small one, know as the ‘epicyclic’
circle. Movements of this kind he attributes to Saturn,
Jupiter, Mars, Venus an Mercury, only not to the Sun. The
Moon he conceives to move in yet another small circle,
— an epicyclic circle of its own.

Figure 1
These
assumptions were due to the Ptolemaic astronomers having
calculated with great care the positions on the Heavens at
which the planets were at given times. They computed these
circling movements so as to understand the fact that the
planets were at given places at given times. It is
astonishing how accurate were the calculations of Ptolemy and
his followers, — relatively speaking at least. Draw the
path of any planet — Mars, for instance — from
modern astronomical data. Compare this 'apparent path',
so-called, of Mars, drawn as observed today, with the path
derived from Ptolemy's theory of deferent and epicyclic
circles. The two curves hardly differ. The difference,
relatively trifling, is only due to the still more accurate
results of modern observation. In point of accuracy these
ancients were not far behind us. That they assumed this queer
system of planetary movements, which seems to us so
complicated, was not due therefore to any faulty observation.
Of course the Copernican system is simpler, — that will
occur to everyone. There is the Sun in the midst, with the
planets moving in circles or ellipses round it. Simple, is it
not? Whereas the other is very complicated: a circular path
superimposed upon another circle, and an eccentric one to
boot.
The Ptolemaic
system was adhered to with a certain tenacity throughout the
Fourth post-Atlantean epoch, and we should ask ourselves this
question: Wherein lies the essential difference in the way of
thinking about cosmic space and the contents of cosmic space,
such as we find it in the Ptolemaic school on the one hand
and in Aristarchus and those who thought like him in the
other? What is the real difference between these ways of
thinking about the cosmic system? It is difficult to describe
popularly, for many things seem outwardly alike, whilst
inwardly they can be very different. Reading Plutarch's
description of Aristarchus system, we shall say: This
heliocentric system is fundamentally no different from the
Copernican. Yet if we enter more deeply into the spirit of
the Aristarchian world-picture, we find it different.
Aristarchus too, no doubt, follows the outer phenomena's with
mathematical lines. In mathematical lines he represents to
himself the movements of the heavenly bodies.
The
Copernican's do likewise. Between the two there intervenes
this other system — the strange one of the Ptolemaic
school. Here it cannot be said that the forming of
mathematical pictures coincides in the same way with what is
observed. The difference in this respect is all-important. In
the Ptolemaic school, the mathematical imagination does not
directly rest upon the sequence of observed points in space.
It is rather like this: In order ultimately to do justice to
them it goes right away from the observed phenomena and works
quite differently, not merely putting the observed results
together. Yet in the end it is found that if one does admit
the mathematical thought-pictures of the Ptolemaic school,
one thereby comprehends what is observed.
Suppose a man
of today were to make a model of the planetary system.
Somewhere he would attach the Sun, them he would draw wires
to represent the orbits of the planets; he would really think
of them as representing the true orbits. In purely
mathematical lines he would comprise the logic of the
planets' paths. Ptolemy would not have done so. He would have
had to construct his model somewhat in this fashion
(Fig. 2).
Here would have been a pivot, fixed to it
a rod, leading to the rim of a rotating wheel, upon this
again another wheel rotating. Such would be Ptolemy's model.
The model he makes, the mathematical picture living in his
thought, is not in the least like what is outwardly seen. For
Ptolemy the Mathematical picture is quite detached from what
is seen externally. And now, in the Copernican system we
return to the former method, simply uniting by mathematical
lines the several places, empirically observed, of the
planet. These mathematical lines correspond to what was there
in Aristarchus's system. Yet is it really the same? This is
the question we must now be asking: Is it the same?
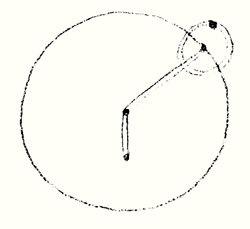
Figure 2
Bearing in
mind the original premises of the Copernican system and the
kind of reasoning by which it is maintained, I think you will
admit: It is just like the way we relate ourselves,
mathematically, to empirical reality in general. You may
confirm it from his works. Copernicus began by constructing
his planetary system ideally, much in the same way as we
construct a triangle ideally and then find it realised in
empirical reality outside us. He took his start from a kind
of a priori mathematical reasoning and them applied it to the
empirically given facts.
What then is
at the bottom of this complicated Ptolemaic system, to make
it so complicated? You remember the well-known anecdote. When
it was shown to Alphonso of Spain, he from his consciousness
of royalty declared: Had God asked his advice at the Creation
of the World, he would have made it more simply than to
require so many cycles and epicycles.
Or is there
something in it after all — in this construction of
cycles and epicycles — related to a real content of
some kind? I put the question to you: Is it only fantasy,
only a thing thought-out, or does this thought out system
after all contain some indication that it relates to a
reality? We can only decide the question by entering into it
in greater detail.
It is like
this. Suppose that with the Ptolemaic system taking you start
from Ptolemaic theories — you follow the movements, or,
as we should say, the apparent movements of the Sun, and of
Mercury, Venus, Mars, Jupiter, and Saturn: to begin with you
will have angular movements of a certain magnitude each time.
You can therefore compare the movements indicated by the
successive positions of these heavenly bodies in the sky. The
Sun has no epicyclic movement. The epicyclic daily movement
of the Sun is therefore zero. For Mercury on the other hand
we must put down a number, representing his daily movement
along his epicyclic circle, which we shall them compare with
that of other planets. Let us call the epicyclic daily
movements —
x3 + x’ = y
x4 + x ’ ’ = y
x5 + x’ ’ ’ = y.
Now take the movements Ptolemy attributes to the centres
of the epicycles along their different circles. Let the daily
movement be y for the Sun. It is then remarkable that if we
seek the corresponding value for Mercury we get precisely the
same figure. The movement of the centre of Mercury's epicycle
equals the movement of the Sun. We must write y again, and so
for Venus. This then holds good of Mercury and Venus. The
centres of their epicycles move along paths which correspond
exactly to the Sun's path, — run paralleled to it. For
Mars, Jupiter and Saturn on the other hand the movements of
the centres of the epicycles are diverse, — shall we
say
x for Mars,
x for Jupiter,
x for Saturn.
Yet the remarkable fact is that by taking
the corresponding sums, namely x3 + x + x4 + x , x5 _ x,
adding the movements along the several epicycles to the
movements of the centres of these epicycles, — I get
the same magnitude for all three planets. Nay more, it is the
identical which we obtained just now for the movement of the
Sun and of the centres of the epicycles of Mercury and Venus
—
x3 + x = y,
x4 + x = y,
x5 + x = y.
A noteworthy
regularity, you see. This regularity will lead us to
attribute a different cosmic significance to the centres at
the epicycles of Venus and Mercury, the planets near the Sun
as they are called, and of Jupiter, Mars, Saturn etc. called
distant from the Sun. For the distant planets, the centre of
the epicycle has not the same cosmic meaning. Something is
there, by virtue of which the whole meaning of the planet's
course is different than for the planets near the Sun.
The fact was
well-known in the Ptolemaic school and helped determine the
whole idea — the peculiar construction of cycles and
epicycles in the mind, detached from the empirically given
facts. This very fact obliged them, as they saw it, to
propound their system, and is implicit in it. The human being
of today would scarcely recognise it there; he listens more
or less obtusely when told how they set up their cycles and
epicycles. To their way of thinking on the other hand the
thought was palpable and eloquent???. If Mercury and Venus
have the same values as Jupiter, Saturn and Mars, yet in
another realm, we cannot treat the matter so simply, with an
indifferent circling motion or the like. A planet, in effect,
is of significance not only within the space it occupies but
outside it. We have not merely to stare at it, fixing its
place in the Heavens and in relation to other celestial
bodies; we must go out of it to the centre of the epicycle.
The centre of its epicycle behaves in space even as the Sun
does. Once more, translated into modern forms of speech, the
Ptolemaists said: For Mercury and Venus the centres of the
epicycles so far as movement is concerned behave in cosmic
space as the Sun itself behaves. Not so the other planets
— Mars, Jupiter and Saturn. They claim another right.
In effect, only when we add their epicyclic movements to
their movements along the deferent, only then do they grow
like the Sun in movement. They therefore are differently
related to the Sun.
This
difference of behaviour in relation to the Sun was what they
really built on in the Ptolemaic system. This among others
was an essential reason for its development. Their aim was
not merely to join the empirically given places in the
Heavens by mathematical lines, building it all into a system
of thought in this way. They were at pains to build a
thought-system on another basis, and what is more, a piece of
true knowledge under-lay their efforts; it is undeniable if
we go into it historically. Modern man naturally says: We
have advanced to the Copernican system, why bother about
these ancient thinkers? He bothers not, but if he did, he
would perceive that this was what the Ptolemaists meant.
'Truth is', they said to themselves, Mars, Jupiter and Saturn
have quite another relation to Man than Mercury and Venus.
What corresponds to them in Man is different. Moreover they
connected Jupiter, Saturn and Mars with the forming of the
human head, Venus and Mercury with the forming of what is
beneath the heart in man. Rather than speak of the head,
perhaps I should put it in these words: they related Jupiter,
Saturn and Mars with the forming of all that is above the
heart; Venus and Mercury with what is situated below the
heart in man. The Ptolemaists did indeed relate to man, what
they were trying to express in their cosmic system.
What
under-lay it really? To gain true judgement on this question,
my dear Friends, I think you should read and mark the inmost
tone and essence of my Riddles of Philosophy, in writing
which I tried to show how very different was the way man met
the world in his life or knowledge before the 15th Century
and after. Since then, if I may use this image we unpeel
ourselves from the world, — we detach ourselves
completely. Before the 15th Century we did not do so. I must
admit, at this point it is difficult to make oneself
understood in the modern world. Man of to-day says to
himself: “I think thus and thus about the world. I have
my sense perceptions, thus or thus. In modern times we have
become enlightened; the men of former times were simple, with
many childish theories.” And as to our enlightenment
and their simplicity the modern man's idea of it amounts to
this, or something very like it: "If only our ancestors had tried
hard enough, they might have grown just as clever as we are.
But it took time, this eduction of mankind; it evidently had
to take some time for men to get as enlightened as they
afterwards became.”
What is today
left unconsidered, is that man's very seeing of the world,
his seeing and his contemplating, his whole relation to the
world was different. Compare the different stages of it,
described in my Riddles of Philosophy. Then you will say:
Through the whole time from the beginning of the Fourth Epoch
until the end, the sharp distinction we now have, of concept
and idea on the one hand and sense-perceived data on the
other, did not exist. They coincided rather. In and with the
sensory quality, men saw the quality of thought, the idea.
And it was ever more so, the farther we go back in them. In
this respect we need more real notions as to the evolution of
mankind. What Dr. Stein has written for example in his book,
upon the essence of sense-perception, is true of our time and
excellently stated. I he had had to write a dissertation on
this subject in the School of Alexandria in olden time, he
would have had to write very differently of sense-perception.
This is what people of today persist in disregarding; they
will have everything made absolute.
And if we go
still farther back, for example into the time when the
Egypto-Chaldean Epoch was at its height, we find an even more
intensive union of concept and idea with sense-perceptible,
outward and physical reality. It was from this moreover
— from this more intensive union — that the
conceptions arose which we still find in Aristarchus of
Samos. They were already decadent in his time; they had been
entertained even more vividly by his predecessors. The
heliocentric system was simply felt, when with their thoughts
and mental pictures men lived in and with the outer
sense-perceptible reality. Then, in the Fourth post-Atlantean
Epoch, man had to get outside the sense-world; he had to wean
himself of this union of his inner life with the sense-world.
In what field was it easiest to do so? Obviously, in the
field where it would seem most difficult to bring the outer
reality and the idea in the mind together. Here was man's
opportunity to wrest himself away — in his life of
ideas — from sense-impressions.
Look at the
Ptolemaic system from this angle; see in it an important
means toward the education of mankind; then only do we
recognise the essence of it. The Ptolemaic system is the
great school of emancipation of human thoughts from
sense-perception. When this emancipation had gone far enough
when a certain degree of the purely inner capacity of thought
had been attained — then came Copernicus. A little
later, I may add, this attainment became even more evident,
namely in Galileo and others, whose mathematical thinking is
in the highest degree abstracted and complicated. Copernicus
presented to himself the facts of which we have been speaking
— the observation of the equality of y at diverse
points in the equation, and, working backward from these
mathematical results, was able to construct his cosmic
system. For the Copernican system is based on these results.
It represents a return, from the ideas now abstractly
conceived, to the external, physically sense-perceptible
reality.
It is most
interesting to witness, how in the astronomical world-picture
above all, mankind gets free of the outer reality. And in
perceiving this, my dear Friends, we also gain a truer
estimate of the returning pathway, — for in a wider
sense we must return. Yet how? Kepler still had a feeling of
it. I have often quoted his rather melodramatic saying, to
the effect: I have stolen the sacred vessels of the Egyptian
Temples to bring them back again to modern man. Kepler's
planetary system, as you know, grew from a highly romantic
conception of how the Universe is built. In deed he feels it
like a renewal of the ancient heliocentric system. Yet the
truth is, the ancient heliocentric system was derived, not
from a mere looking outward with the eyes, but from an inner
awareness, an inner feeling of what was living in the
stars.
The human
being who originally set up the cosmic system, making the Sun
the centre with the Earth circling round it after the manner
of Aristarchus of Samos, felt in his heart the influences of
the Sun, felt in his head the influences of Venus and
Mercury. This was experience, direct experience throughout
the human being, and out of this the system grew. In later
time this all-embracing experience was lost. Perceiving still
with eyes and ears and nose, man could no longer perceive
with heart or liver. To have perception from the Sun with
one's heart, or from Jupiter with one's nose, seems like
sheer madness to the people of today. Yet it is possible and
it is exact and true. Moreover one is well aware why they
think it madness.
This living
with the Universe, intensively and all-awarely, was lost in
course of time. Then Ptolemy conceived a mathematical
world-picture still with a little of the old feeling to begin
with, yet in its essence already detached from the world. The
earlier disciples of the Ptolemaic school still felt, though
very slightly, that it is somehow different with the Sun than
with Jupiter for instance. Later they felt it no more. In
effect the Sun reveals his influence comparatively simply
through the heart. Jupiter, we must admit, spins like a wheel
in our head, — it is the whirling epicycle. Whilst in a
different sense, here indicated
(Fig. 1),
Venus goes through beneath our heart. In later Ptolemaic
times, all they retained of this was the mathematical aspect,
the figure of the circle: the simple circle for the Sun's
path and the more complicated for the planets. Yet in this
mathematical configuration there was at least some remnant of
relation to the human being.
Then even
this was lost and the high tide of abstraction came. Today we
must look for the way back, — to re-establish once
again from the entire Man an inner relation to the Cosmos. We
have not to go on from Kepler, as Newton did, into still
further abstractions. For Newton put abstractions in the
place of things more real; he introduced mass etc. into the
equations — a mere transformation, in effect, yet there
is no empirical fact to vouch for it. We need to take the
other road, whereby we enter reality even more deeply then
Kepler did. And to this end we must include in our ambit what
after all is in its life connected with the rising of the
stars across the Heavens, namely the Kingdoms of external
Nature in all their variedness of form and kind.
Is it not
worthy of note that we find a contrast between the superior
planets so-called and the inferior, with the Earth-entity
between the mineral and plant kingdoms along the one branch,
the animal and man along the other? And, that in drawing the
two branches of the forked line, we must put plant and
mineral in simple prolongation, while animal and man must be
so drawn as to show the formative process returning upon
itself?
(Fig. 3)

Figure 3
We have put
two things and of different kind before us: on the one hand
the paths of the epicycle-centres and of the points on the
epicyclic circumference, revealing a quite different relation
to the Sun for the superior and inferior planets
respectively; on the other hand the prolongation of the
plant-forming process speeding on into the mineral, whilst
the animal-forming process turns back upon itself to become
man. (The symbolism of our diagram is justified; as I said
yesterday, to recognise it you need only make a study of
Selenka's work.)
These two
things side by side we put as problems, and we will try from
thence to reach a cosmic system true to reality.
|